相关习题
0 319392 319400 319406 319410 319416 319418 319422 319428 319430 319436 319442 319446 319448 319452 319458 319460 319466 319470 319472 319476 319478 319482 319484 319486 319487 319488 319490 319491 319492 319494 319496 319500 319502 319506 319508 319512 319518 319520 319526 319530 319532 319536 319542 319548 319550 319556 319560 319562 319568 319572 319578 319586 366461
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 (答案不唯一,只需填一个)
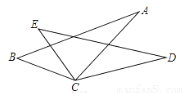
AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定.
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
如图,已知AC=DB,要使△ABC≌△DCB,则需要补充的条件为 .
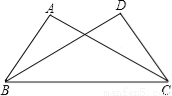
AB=DC(答案不唯一)
【解析】试题分析:本题中有公共边BC=CB,利用SSS来判定全等则只需要添加条件AB=DCA即可
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
如图,AB=AC,要使△ABE≌△ACD,依据ASA,应添加的一个条件是 .
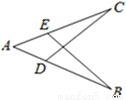
∠C=∠B.
【解析】
试题分析:此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
可添加条件:∠B=∠C,再有条件AB=AC,∠A=∠A可利用ASA证明△ACD≌△ABE.
解...
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E,D,AD=25,DE=17,则BE=______.
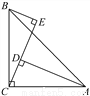
8
【解析】∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
又∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠BCE+∠CBE=90°,
∴∠CBE=∠ACD,
在△CBE和△ACD中,,
∴△CBE≌△ACD(AAS),
∴BE=CD,CE=AD=25,
∵DE=17,
∴CD=CE?DE=AD?DE=25?17...
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
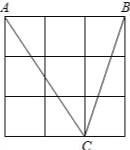
如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形共有 个(不含△ABC).
7.
【解析】
试题分析:本题考查的是用SSS判定两三角形全等.如图所示每个大正方形上都可作两个全等的三角形,所以共有八个全等三角形,除去△ABC外有七个与△ABC全等的三角形.
故答案为:7.
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
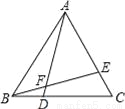
如图,在等边△ABC中,BD=CE,AD与BE相交于点F,则∠AFE=______.
60°
【解析】根据题目已知条件可证△ABD≌△BCE,再利用全等三角形的性质及三角形外角和定理求解.
【解析】
∵等边△ABC,
∴∠ABD=∠C,AB=BC,
在△ABD与△BCE中,,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠ABE+∠EBC=60°,
∴∠ABE+∠BAD=60°,
∴∠APE=∠ABE+∠BAD...
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
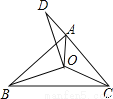
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为 _________ .
60°.
【解析】
试题分析:可证明△COD≌△COB,得出∠D=∠CBO,再根据∠BAC=80°,得∠BAD=100°,由角平分线可得∠BAO=40°,从而得出∠DAO=140°,根据AD=AO,可得出∠D=20°,即可得出∠CBO=20°,则∠ABC=40°,最后算出∠BCA=60°
试题解析:∵△ABC三个内角的平分线交于点O,
∴∠ACO=∠BCO,
在△CO...
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
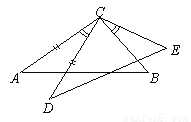
如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是______.(填写一个即可,不得添加辅助线和字母)
∠A=∠D或∠B=∠E或BC=EC
【解析】A=∠D,
理由是:∵∠ACD=∠BCE,
∴∠ACD+∠DCB=∠BCE+∠DCB,
∴∠ACB=∠DCE,
在△ACB和△DCE中,
∴△ACB≌△DCE(ASA),
故答案为:∠A=∠D.
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E,在BC上,BE=BF,连结AE,EF和CF,此时,若∠CAE=30°,那么∠EFC=_______.
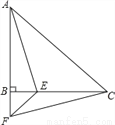
30°
【解析】在△ABE和△CBF中,
∵,
∴△ABE≌△CBF(SAS),
∵AB=BC,∠ABC=90°,∠CAE=30°,
∴∠CAB=∠ACB=12(180°?90°)=45°,∠EAB=45°?30°=15°.
∵△ABE≌△CBF,
∴∠EAB=∠FCB=15°.
∵BE=BF,∠EBF=90°,
∴∠BFE=∠FEB=45°....
查看答案和解析>>
科目:
来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案)
题型:填空题
如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=___________度.
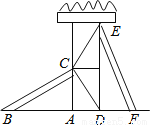
90
【解析】求和的两个角,分别在直角△ABC,直角△DEF中,可以考虑这两个三角形全等,利用全等三角形对应角相等,把两个角转化到同一个三角形中求和.
【解析】
∵BC=EF,AC=DF,∠BAC=∠EDF=90°,∴△BAC≌△EDF(HL).∴∠DFE=∠BCA.
△ABC中,∠ABC+∠BCA=90°,∴∠ABC+∠DFE=90°. 故答案为:90.
查看答案和解析>>










