
科目: 来源:人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型:解答题
已知一次函数y=ax+b的图象上有两点A、B,它们的横坐标分别是3,-1,若二次函数y=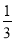 x2的图象经过A、B两点.
x2的图象经过A、B两点.
(1)请求出一次函数的表达式;
(2)设二次函数的顶点为C,求△ABC的面积.
(1);(2)2. 【解析】 试题分析:(1)将A、B的横坐标代入抛物线的解析式中,即可求得A、B的坐标,然后将它们代入直线的解析式中,可得方程组,解方程组即可求得a、b的值,从而得一次函数的表达式;(2)抛物线y=x2的顶点是原点O,设直线AB与x轴的交点为D,先根据直线AB的解析式求出D点坐标,然后根据△ADO的面积减去△OBD的面积=△OAB的面积即可求得. △OAB的面积...查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:填空题
矩形是轴对称图形,对角线是它的对称轴.( )
× 【解析】矩形是轴对称图形,对边中点连线所在的直线是它的对称轴,对角线不是它的对称轴, 故原语句是错误的.查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:填空题
平行四边形也是轴对称图形其对称轴也是对角线.( )
× 【解析】平行四边形不是 但是特殊的平行四边形,如矩形、菱形、正方形等是轴对称图形,但一般的平行四边形不是轴对称图形, 所以原语句是错误的.查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:填空题
AD是直角三角形ABC的中线,那么AD就等于它斜边BC的一半.( )
× 【解析】直角三角形斜边中线等于斜边的一半,已知中只知道三角形ABC是直角三角形,但是没有说明哪个角是直角,只有当∠BAC是直角时,原语句才正确,如果不是,则原语句错误, 所以原语句是错误的.查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
矩形ABCD的长为5,宽为3,点E、F将AC三等分,则△BEF的面积为( ).
A. 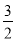 B.
B. 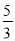 C.
C. 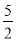 D. 5
D. 5
查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
已知矩形ABCD的AB=2BC,在CD上取点E,使AE=EB,那么∠EBC等于( ).
A. 60° B. 45° C. 30° D. 15°
B 【解析】作EM⊥AB于M , ∵AE=BE, ∴M为AB中点 , ∵AB=2BC, ∴AM=BM=EM , ∴∠MBE=∠MEB=45°, ∴∠EBC=45°, 故选B.查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
已知E、F分别是矩形ABCD的对边BC和AD上的点,且BE=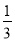 BC,AF=
BC,AF=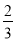 AD,连结AC、EF,那么( ).
AD,连结AC、EF,那么( ).
A. AC平分EF,但EF不平分AC B. AC与EF互相平分
C. EF平分AC,但AC不平分EF D. AC与EF不会互相平分
B 【解析】∵四边形ABCD是矩形,∴AD=BC,AD//BC,∴∠DAC=∠ACB, ∵BE=BC,AF= AD,∴AF=CE, 又∵∠AOF=∠COE,∴△AOF≌△COE, ∴AO=CO,FO=EO,即AC与EF互相平分, 故选B.查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
如果矩形ABCD的对角线AC和BD所成的锐角是60°,那么( ).
A. AC+BD=AB+BC+CD+DA B. BD=2AB
C. AC+BD=AB+BC D. 以上都不对
B 【解析】由矩形ABCD可得AC=BD,且AO=OC=OB=OD,AC和BD所成角为60°,可得AO=BO=CO=DO=AB=DC,只有B选项符合, 故选B.查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
一个矩形和一个平行四边形的边分别相等, 若矩形面积为这个平行四边形的面积的2倍,则平行四边形的锐角的度数为( ).
A. 15° B. 30° C. 45° D. 60°
B 【解析】如图,矩形ABCD与平行四边形BCFG中,BG=AB, 过点G作GH⊥BC,垂足为H, ∵S矩形ABCD=BC·AB=2S平行四边形BCFG=2BC·GH,∴BG=2GH, ∵△BGH是Rt△,∠BHG=90°,∴∠GBH=30°, 故选B.查看答案和解析>>
科目: 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
E为矩形ABCD的边CD上的一点,AB=AE=4,BC=2,则∠BEC是( ).
A. 15° B. 30° C. 60° D. 75°
D 【解析】∵在Rt△ADE中,AD=2,AE=4, ∴∠AED=30°, ∵AB∥CD,∴∠EAB=∠AED=30°, ∵AB=AE, ∴∠AEB=75°, ∴∠BEC=180°-∠AED-∠AEB=180°-30°-75°=75°. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com