
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:单选题
如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
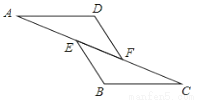
A. ∠A=∠C B. AD=CB C. BE=DF D. AD∥BC
B 【解析】试题分析:求出AF=CE,再根据全等三角形的判定定理判断即可.∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,A、∵在△ADF和△CBE中,∠A=∠C,AF=CE,∠AFD=∠CEB,∴△ADF≌△CBE(ASA),正确,故本选项错误;B、根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项正确;C、∵在△ADF和△CBE中,AF=CE,...查看答案和解析>>
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:单选题
下列条件中,能判定两个直角三角形全等的是( )
A. 一锐角对应相等 B. 两锐角对应相等
C. 一条边对应相等 D. 两条直角边对应相等
D 【解析】试题分析:三角形全等可以利用SAS、SSS、ASA和AAS来进行判定,直角三角形还可以用HL定理来进行判定.本题中D选项可以利用SAS来进行判定三角形全等.查看答案和解析>>
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:填空题
如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是___________.(只需写一个,不添加辅助线)
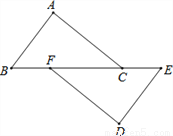
查看答案和解析>>
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:填空题
如图,∠1=∠2,由AAS判定△ABD≌△ACD,则需添加的条件是_______.
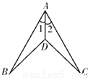
查看答案和解析>>
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:填空题
如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件_____,使得△EAB≌△BCD.
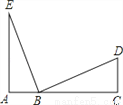
查看答案和解析>>
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:解答题
如图,AB = DE,AC = DF,BE = CF. 求证:AB∥DE.
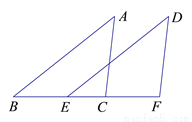
查看答案和解析>>
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:解答题
如图所示,已知AB=DC,AB∥DC,AF=CE.求证:△ABE≌△CDF.
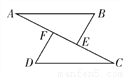
查看答案和解析>>
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:解答题
如图所示,DE⊥AC,BF⊥AC,垂足分别为E,F, DE=BF,AF=CE.求证:AB∥CD.
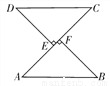
查看答案和解析>>
科目: 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:解答题
如图所示,AB=AC,F,E分别是AB,AC的中点.求证:△ABE≌△ACF.
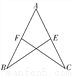
查看答案和解析>>
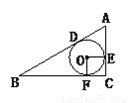
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:填空题
如图,⊙O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com