
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
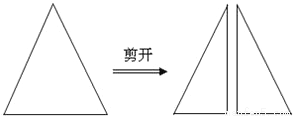
如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有______个不同的四边形.
查看答案和解析>>
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
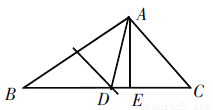
如图,△ABC中,BC=8,AB的中垂线交BC于点D,AC的中垂线交BC于点E,则△ADE的周长等于______.
查看答案和解析>>
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
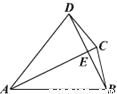
如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号___________(把你认为正确结论的序号都填上)
查看答案和解析>>
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
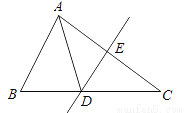
如图,△ABC的周长为19cm,AC的垂直平分线DE交AC于点E,E为垂足,AE=3cm,则△ABD的周长为________.
查看答案和解析>>
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是________°.
15 【解析】因为∠A=50°,AB=AC,所以∠ABC=60°. 因为DE垂直平分AB,所以DA=DB,所以∠DBA=∠A=50°. 所以∠DBC=65°-50°=15°. 故答案为15.查看答案和解析>>
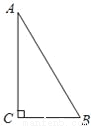
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.
查看答案和解析>>
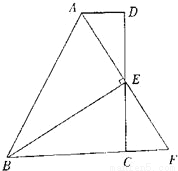
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
查看答案和解析>>
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图所示,在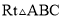 中,∠C=90°,∠A=30°.
中,∠C=90°,∠A=30°.
(1)尺规作图:作线段AB的垂直平分线l(保留作图痕迹,不写作法);
(2)在已作的图形中,若l分别交AB、AC及BC的延长线于点D、E、F,连接BE,求证:EF=2DE.
查看答案和解析>>
科目: 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,已知线段AB,分别以A、B为圆心,大于线段AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC,求∠ADC的度数.
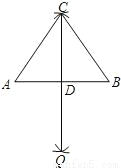
查看答案和解析>>
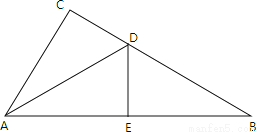
科目: 来源:数学人教版八年级上册13.4课题学习 最短路径问题同步练习题 题型:解答题
有两棵树位置如图,树脚分别为A,B.地上有一只昆虫沿A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处,问小鸟飞至AB之间何处时,飞行距离最短,在图中画出该点的位置.
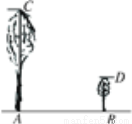
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com