如图，在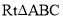中，∠C＝90°，∠B＝30°．AB的垂直平分线DE交AB于点D，交BC于点E，则下列结论不正确的是（　　）

A. AE＝BE B. AC＝BE C. CE＝DE D. ∠CAE＝∠B

B 【解析】A、根据线段垂直平分线的性质，得AE=BE．故该选项正确； B、因为AE＞AC，AE=BE，所以AC＜BE．故该选项错误； C、根据等角对等边，得∠BAE=∠B=30°；根据直角三角形的两个锐角互余，得∠BAC=60°． 则∠CAE=∠BAE=30°，根据角平分线的性质，得CE=DE．故该选项正确； D、根据C的证明过程．故该选项正确． 故选B． ...

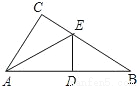
如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（　　）

A. △ABC的三条中线的交点 B. △ABC三边的中垂线的交点

C. △ABC三条角平分线的交点 D. △ABC三条高所在直线的交点

C 【解析】试题分析：要使点到角两边的距离则这个点在这个角的角平分线上.

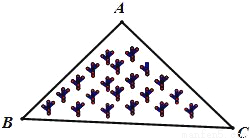
如图，AC＝AD，BC＝BD，则有（　　）

A. AB垂直平分CD B. CD垂直平分AB

C. AB与CD互相垂直平分 D. CD平分∠ACB

A 【解析】试题分析：因为AC=AD，BC=BD，所以点A和点B在线段CD的垂直平分线上，即AB垂直平分CD，故选;A．

如图，在△ABC中，∠B＝30°，ED垂直平分BC，ED＝3．则CE长为（ ）

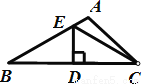
A. 6 B. 9 C. 3 D. 8

A 【解析】因为ED垂直平分BC，所以∠EDB=90°，EB=EC. 因为∠B=30°，∠EDB=90°，所以BE=2DE=6. 所以CE=BE=6. 故选A.

如图，△ABC中，DE垂直平分AC交AB于E，∠A＝30°，∠ACB＝80°，则∠BCE的度数为（ ）

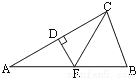
A. 80° B. 70° C. 60° D. 50°

D 【解析】因为DE垂直平分AC，所以EA=EC，∠A=∠ACE. 因为∠A＝30°，所以∠ACE=30°. 所以∠BCE=∠ACB-∠ACE=80°-30°=50°. 故选D.

如图，等腰三角形ABC中，已知AB＝AC，∠A＝30°，AB的垂直平分线交AC于D，则∠CBD的度数为（ ）

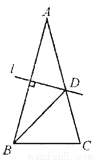
A. 50° B. 30° C. 75° D. 45°

D 【解析】因为AB＝AC，∠A＝30°，所以∠ABC=(180°-30°)÷2=75°， 因为AB的垂直平分线交AC于D，所以DA=DB，所以∠A=∠DBA=30°. 所以∠CBD=∠ABC-∠ABD=75°-30°=45°. 故选D.

如图，在△ABC中，BC边上的垂直平分线DE与边BC交于点D，边AB交于点E．若△EDC的周长为24，△ABC与四边形AEDC的周长之差为12，则线段DE的长为（　　）

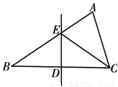
A. 12 B. 6 C. 24 D. 36

B 【解析】因为ED垂直平分BC，所以EB=EC，DB=DC. 因为△ABC与四边形AEDC的周长之差为12， 所以AE+EB+BD+DC+CA-(AE+ED+DC+CA)=12，即BE+BD-DE=12①. 因为CE+CD+DE=24，即BE+BD+DE=24②. ②-①得DE=6. 故选B.

已知A和B两点在线段EF的中垂线上，且∠EBF＝100°，∠EAF＝70°，则∠AEB等于( )

A. 95° B. 15° C. 95°或15° D. 170°或30°

C 【解析】因为A和B两点在线段EF的中垂线上，所以AE=AF，BE=BF， 所以∠AEF=∠AFE，∠BEF=∠BFE. 因为∠EBF＝100°，∠EAF＝70°， 所以∠AEF=(180°-70°)÷2=55°，∠BEF=(180°-100°)÷2=40°. ①当点A，B在EF的同侧时，∠AEB=∠AEF-∠BEF=55°-40°=15°； ②当点A，B在E...

如图，AB＝AC，∠BAC＝120°，AB的垂直平分线交BC于点D，那么∠ADC的度数为（　　）

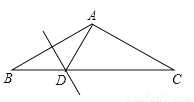
A. 120° B. 30° C. 60° D. 80°

C 【解析】因为AB＝AC，∠BAC＝120°，所以∠B=30°. 因为AB的垂直平分线交BC于点D，所以DB=DA，所以∠B=∠DAB=30°. 所以∠ADC=∠B+∠DAB=30°+30°=60°. 故选C.

如图，∠ABC＝50°，AD垂直且平分BC于点D，∠ABC的平分线BE交AD于点E，连接EC，则∠AEC的度数是（ ）

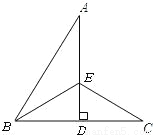
A. 50° B. 25° C. 80° D. 115°

D 【解析】因为AD垂直且平分BC，所以EB=EC，所以∠EBC=∠C. 因为BE平分∠ABC，所以∠ABC=2∠EBC=50°，所以∠EBC=25°，所以∠C=25°. 所以∠AEC=∠C+∠EDC=25°+90°=115°. 故选D.