
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:填空题
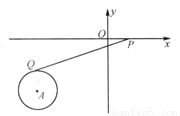
如图所示,在直角坐标系中,A点坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,求P点的坐标为___________.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:解答题
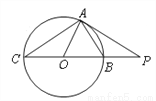
如图,PA为⊙O的切线,A为切点.直线PO与⊙O交于B,C两点,∠P=30°,连接AO,AB,AC.求证:ΔACB≌ΔAPO.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:填空题
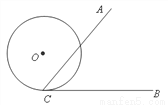
如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O 在CB上向右滚动,则当滚动到⊙O 与CA也相切时,圆心O移动的水平距离是__________cm.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:解答题
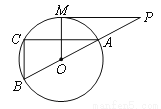
如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,求证:MO∥BC.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:解答题
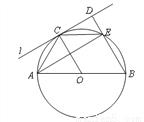
如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E.
(1)求∠AEC的度数;(2)求证:四边形OBEC是菱形.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)测试 题型:单选题
如图,PA、PB分别切⊙O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( )

A. 60° B. 75° C. 105° D. 120°
C 【解析】如图,连接AO,OB, 因为PA,PB分别切圆O于A,B两点, 所以∠PAO=∠PBO=90°, 所以∠AOB=180°-∠P=150°, 设点E是优弧AB上一点, 由圆周角定理可知, ∠E=75°, 由圆内接四边形的对角互补可知, ∠ACB=180°-∠E=105°, 故选C.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)测试 题型:单选题
从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( )
A. 9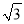 B. 9(
B. 9(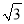 -1) C. 9(
-1) C. 9(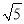 -1) D. 9
-1) D. 9
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)测试 题型:单选题
圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )
A. 180°- 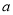 B. 90°-
B. 90°- 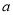 C. 90°+
C. 90°+ 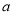 D. 180°-2
D. 180°-2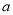
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)测试 题型:填空题
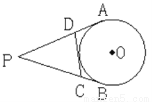
如图,PA、PB分别切圆O于A、B两点,并与圆O的切线分别相交于C、D两点,已知PA=7cm,则△PCD的周长等于_________.
查看答案和解析>>
科目: 来源:2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型:单选题
已知正比例函数的图象过点(2,-3),则该函数图象经过以下的点( )
A. (3,-2) B. (-3,2) C. (-2,3) D. (2,3)
C 【解析】设正比例函数的解析式为y=kx(k≠0),因为正比例函数y=kx的图象经过点(2,-3), 所以-3=2k,解得:k=-,所以y=-x, 当x=3时,y=-4.5,故(-3,2)不在函数图象上; 当x=-3时,y =4.5,故(-3,2)不在函数图象上; 当x=-2时,y=3,故(-2,3)在函数图象上; 当x=2时,y =-3,故(2,3)不在函数...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com