
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:填空题
如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,则BC=___ __cm,∠B=_ __.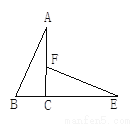
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:填空题
如图,已知点B、C、F、E在同一直线上,∠1=∠2,BC=EF,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是 .(只需写出一个)
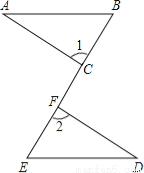
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:填空题
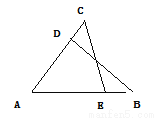
如图,已知∠B=∠C=50°,∠A=60°,则∠AEC=_______;若AE=AD,AB=7,则AC=_____.
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:填空题
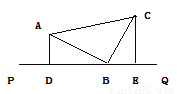
如图,等腰直角三角形ABC的直角顶点B在直线PQ上,AD⊥PQ于点D,CE⊥PQ于点E,且AD=1.7cm,DB=3.3cm,则梯形ADEC的面积是________cm2.
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:填空题
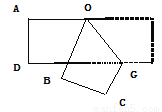
把一张长方形纸条按如图所示折叠得到∠AOB=70°,则∠BOG=______.
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:解答题
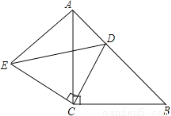
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.求证:BD=AE.
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:解答题
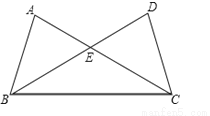
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°,求∠EBC的度数?
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:解答题
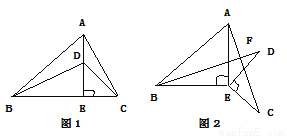
如图1,在△ABC中,AE⊥BC于点E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:解答题
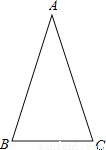
如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
查看答案和解析>>
科目: 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:解答题
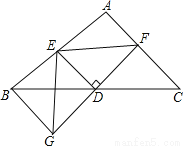
如图,在△ABC中,D是BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连接EG、EF.
(1)求证:BG=CF.
(2)求证:EG=EF.
(3)请判断BE+CF与EF的大小关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com