
科目: 来源:人教版九年级上册数学 25.2用列举法求概率测试 题型:单选题
若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为( )
A. 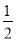 B.
B. 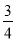 C.
C. 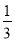 D.
D. 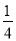
查看答案和解析>>
科目: 来源:人教版九年级上册数学 25.2用列举法求概率测试 题型:单选题
为支援雅安灾区,小慧准备通过爱心热线捐款,她只记得号码的前5位,后三位由5,1,2这三个数字组成,但具体顺序忘记了.他第一次就拨通电话的概率是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:人教版九年级上册数学 25.2用列举法求概率测试 题型:单选题
在x2□2xy□y2的空格□中,分别填上“+”或“-”,在所得的代数式中,能构成完全平方式的概率是( )
A. 1 B. 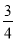 C.
C. 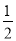 D.
D. 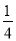
查看答案和解析>>
科目: 来源:人教版九年级上册数学 25.2用列举法求概率测试 题型:填空题
从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是 .
. 【解析】试题分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与随机抽取两个数相乘,积是正数的情况,再利用概率公式求解即可求得答案. 【解析】 画树状图得: ∵共有6种等可能的结果,随机抽取两个数相乘,积是正数的有2种情况, ∴随机抽取两个数相乘,积是正数的概率是:=. 故答案为:.查看答案和解析>>
科目: 来源:人教版九年级上册数学 25.2用列举法求概率测试 题型:填空题
有2名男生和2名女生,王老师要随机地、两两一对地给他们安排座位,1男1女为同桌的概率是 .
【解析】2名男生和2名女生共有六种安排座位的情况,而一男一女为同桌的有4种,所以概率为4÷6=。查看答案和解析>>
科目: 来源:人教版九年级上册数学 25.2用列举法求概率测试 题型:填空题
在平面直角坐标系中,作△OAB,其中三个顶点分别是O(0,0),B(1,1),A(x,y)(-2≤x≤2,-2≤y≤2,x,y均为整数),则所作△OAB为直角三角形的概率是______.
. 【解析】 试题解析:∵A(x,y)(-2≤x≤2,-2≤y≤2,x,y均为整数), ∴A点坐标可以为: (-2,-1),(-2,0),(-2,1),(-2,2), (-1,-2),(-1,0),(-1,1),(-1,2), (0,-2),(0,-1),(0,1),(0,2), (1,-2),(1,-1),(1,0),(1,2), (2,-2),(...查看答案和解析>>
科目: 来源:人教版九年级上册数学 25.2用列举法求概率测试 题型:解答题
某商场开展购物抽奖活动,抽奖箱中有4个标号分别为1,2,3,4的质地、大小相同的小球,顾客任意摸取一个小球,然后放回,再摸取一个小球,若两次摸出的数字之和为“8”是一等奖,数字之和为“6”是二等奖,数字之和为其他数字则是三等奖,请分别求出顾客抽中一、二、三等奖的概率.
, , . 【解析】【解析】 画树状图得: ∵共有16种等可能的结果,两次摸出的数字之和为“8”的有1种情况,数字之和为“6”的有3种情况, ∴P(一等奖)=,P(二等奖)=,P(三等奖)=1--=. 故答案为: , , .查看答案和解析>>
科目: 来源:人教版九年级上册数学 25.2用列举法求概率测试 题型:解答题
甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学举行首场比赛.求下列事件的概率:
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学.
(2)随机选取2名同学,其中有乙同学.
(1); (2). 【解析】试题分析:(1)根据一共有3种等可能性的结果,其中恰好选中乙同学的有1种,根据概率公式即可求得答案。 (2)先求出全部情况的总数,再求出符合条件的情况数目,二者的比值即为事件的概率。 试题解析:(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学的概率是 。 (2)从甲、乙、丙、丁4名同学中随机选取2名同学,所有可能出现的结果有...查看答案和解析>>
科目: 来源:同步练习3:1.1菱形的性质与判定 题型:单选题
下列命题中,真命题是( )
A. 对角线互相垂直且相等的四边形是菱形
B. 对角线互相垂直的平行四边形是菱形
C. 对角线互相平分且相等的四边形是菱形
D. 对角线相等的四边形是菱形
B 【解析】试题分析:A.不能判断是否为菱形,故A错误; B.对角线互相垂直的平行四边形是菱形,正确; C.对角线相等且互相平分的四边形是矩形,故C错误; D.不能判断是否为菱形;故D错误; 故选B.查看答案和解析>>
科目: 来源:同步练习3:1.1菱形的性质与判定 题型:单选题
菱形的周长为12 cm,相邻两角之比为5∶1,那么菱形对边间的距离是( )
A.6 cm B.1.5 cm C.3 cm D.0.75 cm
B 【解析】 试题分析:作AE⊥BC,根据菱形的周长可以计算菱形的边长,根据含30°角的直角三角形的性质即可得到AB=2AE,从而得到结果. 作AE⊥BC, 菱形的周长为12cm,则AB=3cm, 相邻两角之比为5:1,且两角之和为180°, ∴∠B=30°, 在Rt△ABE中,AB=3cm,∠B=30° ∴AE=1.5cm, 故选 B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com