
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:填空题
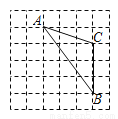
如图,在正方形网格中,△ABC的顶点都在格点上,则cos∠ABC的值为__________.
查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:填空题
如图,在□ABCD中,E、F分别是AB、AD的中点,EF交AC于点G,则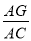 的值是__________.
的值是__________.
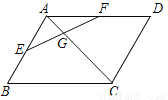
查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:填空题
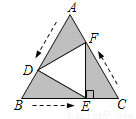
如图,在等边△ABC中,点D、E、F分别以相同的速度同时由点A、B、C向点B、C、A运动,当EF⊥BC时,△DEF与△ABC的面积比为__________.
查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
(5分)求值:2 cos60°+2 sin30°+4tan45°.
6. 【解析】试题分析:将特殊角的三角函数值代入计算即可. 试题解析:原式= =6.查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
不解方程,判断下列方程的根的情况:
(1)x2+2x﹣2=0.
(2)4x2﹣x+4=0.
(1) 有两个不相等的实数根;(2)方程没有实数根. 【解析】试题分析:分别计算根的判别式,利用根的判别式的符号进行判断即可. 试题解析:(1)∵△=22﹣4×1×(﹣2)=12>0, ∴方程有两个不相等的实数根; (2)∵△=(﹣1)2﹣4×4×4=﹣63<0, ∴方程没有实数根.查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
解下列方程:
(1)x2﹣3x=1.
(2)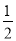 (y+2)2﹣6=0.
(y+2)2﹣6=0.
查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
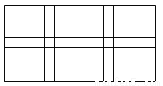
(6分)如图,学校课外生物小组的试验园地是长40 m、宽20m的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道,要使种植面积为648m2,求小道的宽.
查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
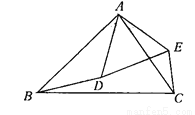
(6分)如图, 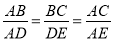 .求证:∠ BAD=∠CAE.
.求证:∠ BAD=∠CAE.
查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
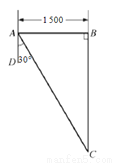
(6分)如图,在相距1 500米的东、西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东30°的方向,在炮台B处测得敌舰C在它的正南方.试求敌舰与两炮台的距离.
查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
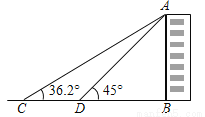
(7分)某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.要测量学校一幢教学楼AB的高度如图所示,他们先在点C测得教学楼的顶部A的仰角为36.2°,然后向教学楼前进10米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼AB的高度.(结果精确到1米)
【参考数据:sin36.2°=0.59,cos36.2°=0.81,tan36.2°=0.73】
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com