
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:填空题
抛物线y=x2+bx+c与x轴无公共点,则b2与4c的大小关系是_________.
b2<4c. 【解析】试题解析:∵抛物线y=x2+bx+c与x轴无公共点, ∴方程x2+bx+c=0无解, ∴△<0, 即b2-4c<0, ∴b2<4c.查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:填空题
已知a:b=3:2,则(a-b):a= .
. 【解析】 试题分析:根据比例关系即可得到答案. ∵a:b=3:2 ∴(a-b):a=(3-2):3=1:3查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:填空题
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为________米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).
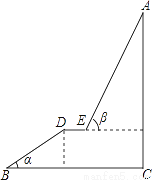
查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:解答题
如果二次根式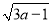 与
与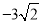 能够合并,能否由此确定a=1?若能,请说明理由;不能,请举一个反例说明.
能够合并,能否由此确定a=1?若能,请说明理由;不能,请举一个反例说明.
查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:解答题
如图,用一根6米长的笔直钢管弯折成如图所示的路灯杆ABC,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,若路灯杆顶端C到地面的距离CD=5.5米,求AB长.
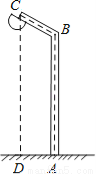
查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:解答题
平面直角坐标中,对称轴平行于y轴的抛物线经过原点O,其顶点坐标为(3,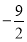 );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(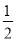 ,0),且BC=5,AC=3(如图1).
,0),且BC=5,AC=3(如图1).
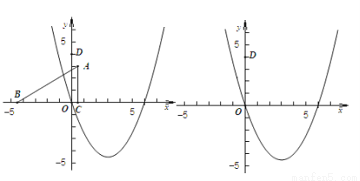
图1 图2
(1)求出该抛物线的解析式;
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动.D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s.
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图1、图2中画出探求);
②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由.
(1)y=x2﹣3x; (2)①当点B位于原点左侧时,S=m+10.(﹣4.5≤m<0), 当点B位于原点右侧(含原点O)时,S=m+10.(0≤m<﹣2), ②存在,m1=﹣1,m2=﹣4,m3=﹣4.4. 【解析】 试题分析:(1)根据抛物线顶点坐标为(3,﹣),利用顶点式求出即可; (2)根据当点B位于原点左侧时以及当点B位于原点右侧(含原点O)时,分别分...查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:解答题
(2013•朝阳)如图1,在综合实践活动中,同学们制作了两块直角三角形硬纸板,一块含有30°角,一块含有45°角,并且有一条直角边是相等的.现将含45°角的直角三角形硬纸板重叠放在含30°角的直角三角形硬纸板上,让它们的直角完全重合.如图2,若相等的直角边AC长为12cm,求另一条直角边没有重叠部分BD的长(结果用根号表示).
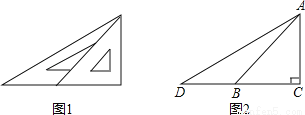
查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:解答题
根据条件求二次函数的解析式:
(1)抛物线的顶点坐标为(﹣1,﹣1),且与y轴交点的纵坐标为﹣3
(2)抛物线在x轴上截得的线段长为4,且顶点坐标是(3,﹣2).
(1)y=﹣2x2﹣4x﹣3;(2)y=x2﹣3x+ 【解析】试题分析:应用待定系数法,求出每个二次函数的解析式各是多少即可. 试题解析:(1)∵抛物线的顶点坐标为(﹣1,﹣1), ∴设抛物线的解析式为:y=a(x+1)2﹣1, ∵抛物线与y轴交点的纵坐标为﹣3, ∴﹣3=a(0+1)2﹣1, 解得a=﹣2. ∴抛物线的解析式是y=﹣2(x+1)2﹣1, ...查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:解答题
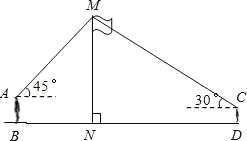
如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(45°)是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D)在同一条直线上).请求出旗杆MN的高度.(参考数据: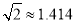 ,
,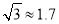 ,结果保留整数)
,结果保留整数)
查看答案和解析>>
科目: 来源:山西省2018届九年级上期末模拟数学试卷 题型:解答题
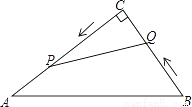
如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
(1)几秒后P,Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1,△ABC的面积为S2,在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com