在Rt△POQ中，OP=OQ=4，M是PQ中点，把一三角尺的直角顶点放在点M处，以M为旋转中心，旋转三角尺，三角尺的两直角边与△POQ的两直角边分别交于点A、B．

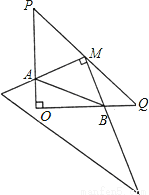
（1）求证：MA=MB；

（2）连结AB，探究：在旋转三角尺的过程中，△AOB的周长是否存在最小值？若存在，求出最小值；若不存在，请说明理由．

（1）证明见解析；（2）有最小值，最小值为4+2． 【解析】 试题分析：（1）过点M作ME⊥OP于点E，作MF⊥OQ于点F，可得四边形OEBF是矩形，根据三角形的中位线定理可得ME=MF，再根据同角的余角相等可得∠AME=∠BMF，再利用“角边角”证明△AME和△BMF全等，根据全等三角形对应边相等即可证明； （2）根据全等三角形对应边相等可得AE=BF，设OA=x，表示出AE为...

如图，点A是反比例函数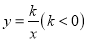 图像上的一点，过点A作AB⊥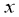轴于点B，且△AOB的面积为2，点A的坐标为．

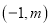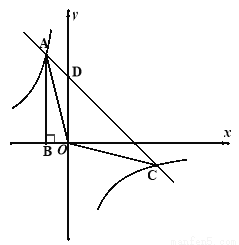
（1）求m和k的值．

（2）若一次函数y=ax+3的图像经过点A，交双曲线的另一支于点C，交y轴于点D，求△AOC的面积．

（3）在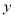轴上是否存在点P，使得△PAC的面积为6？如果存在，请求出点P的坐标；若不存在，请说明理由．

（1）m=4，k=-4；（2）；（3）存在，P点坐标为（0，）或（0，）． 【解析】 试题分析：（1）△AOB的面积为2，点A的坐标为（-1，m）得，求出m的值，把点A坐标代入求得k的值即可；（2）把A（-1,4）代入y=ax+3求出一次函数的表达式，联立，解方程组求出点C的坐标，进而求出△AOC的面积；（3）假设存在，设P点坐标为（0，c）有：=6，进而求出c的值即可． 试题解...

已知：抛物线y=ax2+bx+c经过A（-1，0）、B（3，0）、C（0，3）三点，直线l是抛物线的对称轴，M为它的顶点

（1）求抛物线的函数关系式；

（2）求△MCB的面积；

（3）设点P是直线l上的一个动点，当PA+PC最小时，求最小值．

（1）抛物线的函数关系式为y=-x2+2x+3；（2）3；（3） 【解析】试题分析：（1）根据待定系数法求出抛物线解析式； （2）先求出直线BC与对称轴的交点，即可得出MN，再用面积之和即可得出结论； （3）先根据抛物线的对称性，判断出点P是直线BC与抛物线的对称轴l的交点，根据（2）直接得出点P坐标． 试题解析：（1）∵抛物线y=ax2+bx+c经过A（-1，0）、B（...

如图，某农户为了发展养殖业，准备利用一段墙（ 墙长18米）和55米长的竹篱笆围成三个相连且面积相等的长方形鸡、鸭、鹅各一个．问：

（1）如果鸡、鸭、鹅场总面积为150米2，那么有几种围法？

（2）如果需要围成的养殖场的面积尽可能大，那么又应怎样围，最大面积是多少？

（1）垂直于墙的竹篱笆长10米，平行于墙的竹篱笆长15米，只有1种围法 （2）垂直于墙的竹篱笆长9.25米，平行于墙的竹篱笆长18米,最大面积166.5米2． 【解析】本题考查了一元二次方程的应用. （1）设出竹篱笆围成长方形的宽为x米，则长为（55-4x）米，利用长方形的面积解答即可；（2）设出养殖场的面积为S，考虑墙长18米，即可解决问题． 【解析】 （1）设竹篱笆围成长方...

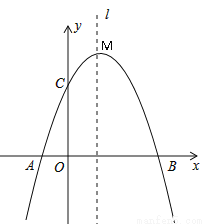
△ABC的内切圆⊙o与BC，CA，AB分别相切于点D、E、F，且AB=9cm，BC=14cm，CA=13cm，求AF、BD、CE的长？

AF=4cm，BD=5cm，CE=9cm． 【解析】试题分析：根据切线长定理，可设AE=AF=xcm，BF=BD=ycm，CE=CD=zcm．再根据题意列方程组，即可求解． 【解析】 根据切线长定理，设AE=AF=xcm，BF=BD=ycm，CE=CD=zcm． 根据题意，得 ， 解得： ． 即AF=4cm、BD=5cm、CE=9cm．

如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AC=13，BC=5，BE⊥DC交DC的延长线于点E．

（1）求证：CB是∠ECA的角平分线；

（2）求DE的长；

（3）求证：BE是⊙O的切线．

（1）证明见解析；（2）．（3）证明见解析． 【解析】 试题分析：（1）根据BD=BA得出∠BDA=∠BAD，再由∠BCA=∠BDA即可得出结论； （2）判断△BED∽△CBA，利用对应边成比例的性质可求出DE的长度． （3）连接OB，OD，证明△ABO≌△DBO，推出OB∥DE，继而判断BE⊥OB，可得出结论． 试题解析：（1）∵BD=BA， ∴∠BDA=∠B...

（10分）一块直角三角形木版的一条直角边AB为3m，面积为6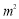，要把它加工成一个面积最大的正方形桌面，小明打算按图①进行加工，小华准备按图②进行裁料，他们谁的加工方案符合要求?

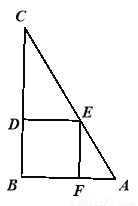
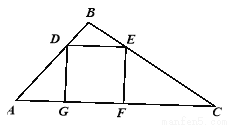
图① 图②

所以小明同学的方法符合要求. 【解析】 试题分析：根据题意必须首先求得正方形的边长．图1中，根据相似三角形对应边的比相等即可求得；图2中，根据相似三角形对应高的比等于相似比即可求得． 试题解析：由AB＝3m，△ABC的面积为6m2，得BC＝4m． 如图①，设小明加工的桌面边长为xm，由DE∥AB，得,即，解得：x＝（m） 如图②，过点B作BH⊥AC，分别交DE、AC于...

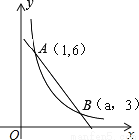
（2015秋•岳池县期末）如图，直线y=k1x+b与反比例函数y=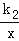（x＞0）的图象交于A（1，6），B（a，3）两点．

（1）求k1和k2的值；

（2）结合图象直接写出k1x+b﹣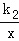＞0的x的取值范围．

（1）k2=，（2）1＜x＜2． 【解析】 试题分析：（1）先把A（1，6）代入y=得到k2=1×6=6，再把B（3，a）代入y=得a=2，则B点坐标为（2，3），然后利用待定系数法求一次函数的解析式，得到k1的值； （2）根据函数的图象结合A、B的坐标即可求得． 【解析】 （1）∵直线y=k1x+b与反比例函数y=（x＞0）的图象交于A（1，6），B（a，3）两点， ...

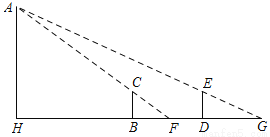
如图，操场上有一根旗杆AH，为测量它的高度，在点B和点D处各立一根高1.5米的标杆BC、DE，且BD=30米，测得视线AC与地面HG的交点为F，视线AE与地面HG的交点为G，且H、B、F、D、G都在同一直线上，测得BF=3米，DG=5米，求旗杆AH的高度.

24m 【解析】试题分析：首先设AH=x，BH=y，根据△AHF∽△CBF，△AHG∽△EDG，得出， ，然后将各数字代入求出x的值. 试题解析：由题意知，设AH=x，BH=y， △AHF∽△CBF，△AHG∽△EDG， ∴， ， ∴3x=1.5×（y+3）， 5x=1.5×（y+30+5） 解得x=24m． 答：旗杆AH的高度为24m． ...

大润发超市以每件30元的价格购进一种商品，试销中发现每天的销售量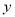（件）与每件的销售价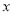（元）之间满足一次函数.

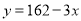（1）、写出超市每天的销售利润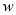（元）与每件的销售价x（元）之间的函数关系式；

（2）、如果超市每天想要获得销售利润420元，则每件商品的销售价应定为多少元？

（3）、如果超市要想获得最大利润，每件商品的销售价定为多少元最合适？最大销售利润为多少元？

（1）、w=－3+252x－4860；（2）、40或44；（3）、42元，432元. 【解析】 试题分析：（1）、根据销售利润=单件利润×数量求出；（2）、根据w=420列出一元二次方程，求出x的值；（3）、将二次函数配方成顶点式，然后进行说明. 试题解析：（1） ∴ （2）由题意知： ∴ ∴ ∴当销售价定为40或44元时，可获得420元的利润. （...