
科目: 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
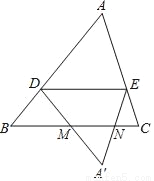
如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若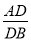 =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.
(3)若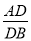 =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
查看答案和解析>>
科目: 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
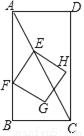
如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒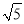 个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
(1)用含t的代数式表示点E到边AB的距离.
(2)当点G落在边AB上时,求t的值.
(3)连结BG,设△BFG的面积为S平方单位(S>0),求S与t之间的函数关系式.
(4)直接写出当正方形EFGH的顶点与点B,D距离相等时的t值.
查看答案和解析>>
科目: 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
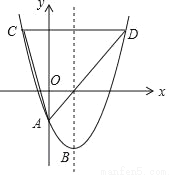
如图,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣4与y轴交于点A,顶点为B,点A的坐标为(0,﹣2),点C在抛物线上(不与点A,B重合),过点C作y轴的垂线交抛物线于点D,连结AC,AD,CD,设点C的横坐标为m.
(1)求这条抛物线所对应的函数表达式.
(2)用含m的代数式表示线段CD的长.
(3)点E是抛物线对称轴上一点,且点E的纵坐标比点C的纵坐标小1,连结BD,DE,设△ACD的面积为S1,△BDE的面积为S2,且S1•S2≠0,求S2=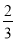 S1时m的值.
S1时m的值.
(4)将抛物线y=a(x﹣2)2﹣4沿x=2平移,得到抛物线y=a(x﹣2)2+k,过点C作y轴平行线与抛物线y=a(x﹣2)2+k交于点F,若CD与y轴交于点G,且CD=6,直接写出使AC=FG的点F的坐标.
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
在实数π、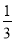 、
、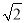 、0.1234中,无理数的个数为( )
、0.1234中,无理数的个数为( )
A. 1 B. 2 C. 3 D. 4
B 【解析】根据无理数的概念,无限不循环小数是无理数,可知π、是无理数. 故选:B.查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是
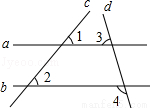
A.35° B.70° C.90° D.110°
D查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000001米,那么数据0.0000025用科学记数法可以表示为( )
A. 2.5×105 B. 2.5×106 C. 2.5×10﹣5 D. 2.5×10﹣6
D 【解析】由科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.因此0.0000025=2.5×10﹣6. 故选:D. 此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<1...查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图是一个三视图,则它所对应的几何体是( )
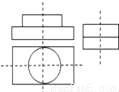
A. 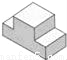 B.
B. 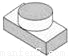 C.
C. 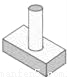 D.
D. 
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
下列运算正确的是( )
A.a2+a3=a5 B.a2•a3=a6 C.(a2b3)3=a5b6 D.(a2)3=a6
D. 【解析】 试题解析:A、a2与a3不是同类项不能合并,故本选项错误; B、应为a2•a3=a5,故本选项错误; C、应为(a2b3)3=a6b9,故本选项错误; D、(a2)3=a6,正确; 故选D.查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
我们这样来探究二次根式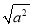 的结果,当a>0时,如a=3,则
的结果,当a>0时,如a=3,则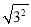 =3,此时
=3,此时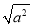 的结果是a本身;当a=0时,
的结果是a本身;当a=0时, 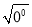 =0.此时
=0.此时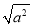 的结果是零;当a<0时,如a=﹣3,则
的结果是零;当a<0时,如a=﹣3,则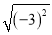 =﹣(﹣3)=3,此时
=﹣(﹣3)=3,此时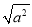 的结果是a的相反数.这种分析问题的方法所体现的数学思想是( )
的结果是a的相反数.这种分析问题的方法所体现的数学思想是( )
A. 分类讨论 B. 数形结合 C. 公理化 D. 转化
A 【解析】根据题意可知,探究过程是分三种情况讨论的,因此可知体现了数学思想是:分类讨论. 故选:A查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
济南某中学足球队的18名队员的年龄如表所示:
年龄(单位:岁) |
| 12 |
| 13 |
| 14 |
| 15 |
人数 |
| 3 |
| 5 |
| 6 |
| 4 |
这18名队员年龄的众数和中位数分别是( )
A.13岁,14岁 B.14岁,14岁 C.14岁,13岁 D.14岁,15岁
B 【解析】试题分析:∵济南某中学足球队的18名队员中,14岁的最多,有6人, ∴这18名队员年龄的众数是14岁; ∵18÷2=9,第9名和第10名的成绩是中间两个数, ∵这组数据的中间两个数分别是14岁、14岁, ∴这18名队员年龄的中位数是:(14+14)÷2=28÷2=14(岁) 综上,可得这18名队员年龄的众数是14岁,中位数是14岁. 故选:B....查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com