
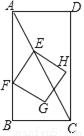
如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒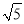 个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
(1)用含t的代数式表示点E到边AB的距离.
(2)当点G落在边AB上时,求t的值.
(3)连结BG,设△BFG的面积为S平方单位(S>0),求S与t之间的函数关系式.
(4)直接写出当正方形EFGH的顶点与点B,D距离相等时的t值.
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(2) 题型:解答题
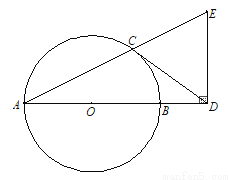
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=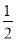 ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:单选题
在学校开展的“爱我中华”的一次演讲比赛中,编号1,2,3,4,5,6的五位同学最后成绩如表所示.那么这五位同学演讲成绩的众数与中位数依次是( )
参赛者编号 | 1 | 2 | 3 | 4 | 5 | 6 |
成绩/分 | 95 | 88 | 90 | 93 | 88 | 92 |
A. 92,88 B. 88,90 C. 88,92 D. 88,91
D 【解析】由表可知,这6为同学的成绩分别为:88、88、90、92、93、95, 则众数为88,中位数为(90+92) ÷2=91, 故选:D.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
正比例函数y=(a+1)x的图象经过第二、四象限,若a同时满足方程x2+(1﹣2a)x+a2=0,则此方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 不能确定
A查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图是一个三视图,则它所对应的几何体是( )
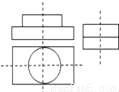
A. 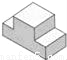 B.
B. 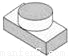 C.
C. 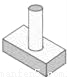 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
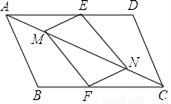
如图,在?ABCD中,点E,F分别在边AD,BC上,点M,N在对角线AC上,且AE=CF,AM=CN,求证:四边形EMFN是平行四边形.
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:填空题
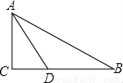
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若∠B=30°,BD=6,则CD的长为_____.
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
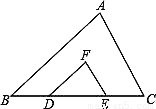
如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
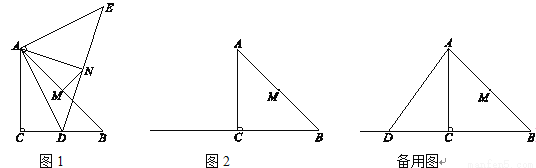
在△ABC中,∠ACB=90°,AC=BC=4,M为AB的中点.D是射线BC上一个动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED,N为ED的中点,连接AN,MN.
(1)如图1,当BD=2时,AN=___ __,NM与AB的位置关系是____ _____;
(2)当4<BD<8时,
①依题意补全图2;
②判断(1)中NM与AB的位置关系是否发生变化,并证明你的结论;
(3)连接ME,在点D运动的过程中,当BD的长为何值时,ME的长最小?最小值是多少?请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com