
科目: 来源:2017年海南省中考数学模拟试卷 题型:填空题
一个两位数,十位上的数字比个位上的数字大7,且十位上的数字与个位上的数字和的平方等于这个两位数,这个两位数是_____.
81 【解析】试题解析:设个位上的数为x,则十位上的数为x+7, 依题意,得(x+7+x)2=10(x+7)+x, 整理得:4x2+17x-21=0, 解得:x1=1,x2=-(舍去), 所以,x=1,x+7=8. 故这个两位数是81.查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷 题型:填空题
如图,已知点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=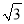 ,则?ABCD面积的最大值为_____.
,则?ABCD面积的最大值为_____.
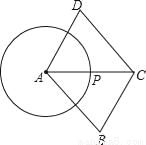
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷 题型:填空题
如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于_____.
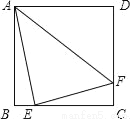
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷 题型:解答题
﹣22÷(﹣1)2﹣ ×[4﹣(﹣5)2]
×[4﹣(﹣5)2]
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷 题型:解答题
解不等式组: 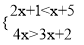 .
.
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷 题型:解答题
已知一个长方形的周长为60cm.
(1)若它的长比宽多6cm,这个长方形的宽是多少cm?
(2)若它的长与宽的比是2:1,这个长方形的长是多少cm?
(1)这个长方形的宽是12cm;(2)这个长方形的长是20cm. 【解析】试题分析:(1)设长方形的宽为xcm,则长为(x+6)cm,根据长方形的周长为60cm列出方程解答即可; (2)设长方形的宽为acm,则长为2acm,根据长方形的周长为60cm列出方程解答即可. 试题解析:(1)设长方形的宽为xcm,则长为(x+6)cm,由题意得 2[x+(x+6)]=60, 解得...查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷 题型:解答题
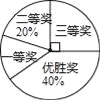
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷 题型:解答题
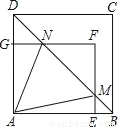
如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证: 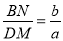 ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷 题型:解答题
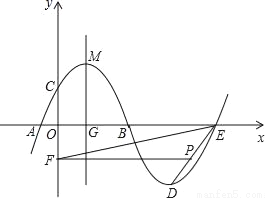
如图,抛物线m:y=﹣0.25(x+h)2+k与x轴的交点为A,B,与y轴的交点为C,顶点为M(3,6.25),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D.
(1)求抛物线n的解析式;
(2)设抛物线n与x轴的另一个交点为E,点P是线段DE上一个动点(P不与D,E重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为(x,y),△PEF的面积为S,求S与x的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)设抛物线m的对称轴与x轴的交点为G,以G为圆心,A,B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com