
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
计算(﹣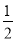 xy2)3,结果正确的是( )
xy2)3,结果正确的是( )
A. 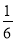 x3y5 B. ﹣
x3y5 B. ﹣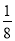 x3y6 C.
x3y6 C. 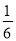 x3y6 D. ﹣
x3y6 D. ﹣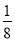 x3y5
x3y5
查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列式子:① 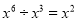 ;②
;②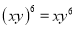 ;③
;③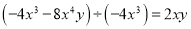 ;④
;④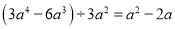 .其中计算不正确的有( )
.其中计算不正确的有( )
A. 3个 B. 2个 C. 1个 D. 0个
A 【解析】试题分析:①、同底数幂除法,底数不变,指数相减,原式=,则错误;②、积的乘方,原式=,则错误;③、根据同底数幂的除法分别进行计算,原式=1+2xy,则错误;④、计算正确,故选A.查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
已知点P(-2,1),那么点P关于x轴对称的点P′的坐标是( )
A. (-2,1) B. (-2,-1) C. (-1,2) D. (2,1)
B 【解析】试题分析:点的坐标关于x轴对称,则对称点坐标也关于x轴对称,横坐标不变,纵坐标变为相反数。故P 坐标为(-2,-1),选B.查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
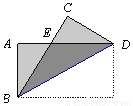
如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:
①△EBD是等腰三角形,EB=ED ;
②折叠后∠ABE和∠CBD一定相等;
③折叠后得到的图形是轴对称图形;
④△EBA和△EDC一定是全等三角形.
其中正确的有( )
A、1个 B、2个 C、3个 D、4个
C. 【解析】 试题分析:根据折叠的性质和平行线的性质可得∠EBD=∠EDB,根据AAS易证△EBA与△EDC全等,①③④是正确,故答案选C.查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
到三角形三顶点距离相等的点是( ),到三角形三边距离相等的点是( )
A. 三条角平分线的交点,三条垂直平分线的交点
B. 三条角平分线的交点,三条中线的交点
C. 三条垂直平分线的交点,三条中线的交点
D. 三条垂直平分线的交点,三条角平分线的交点
D 【解析】试题分析:到三角形三个顶点矩形相等的点在三条中垂线的交点处,到三角形三边距离相等的点在三条角平分线的交点处.故选D.查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
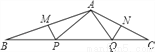
如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于( )
A. 50° B. 75° C. 80° D. 105°
C 【解析】试题分析:根据三角形内角和定理可得:∠B+∠C=180°-130°=50°,根据中垂线的性质可得:∠BAP=∠B,∠CAQ=∠C,则∠BAP+∠CAQ=∠B+∠C=50°,则∠PAQ=∠BAC-(∠BAP+∠CAQ)=130°-50°=80°,故选C.查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=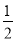 AC•BD,其中正确的结论有( )
AC•BD,其中正确的结论有( )
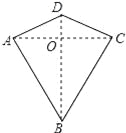
A. 0个 B. 1个 C. 2个 D. 3个
D 【解析】试题分析:在△ABD与△CBD中, ,可得△ABD≌△CBD(SSS),故①正确; 根据全等三角形的性质,可得∠ADB=∠CDB,在△AOD与△COD中, ,可得△AOD≌△COD(SAS),可得∠AOD=∠COD=90°,AO=OC,根据垂直的定义可得AC⊥DB,故②正确; 四边形ABCD的面积= =ACBD,故③正确; 故选D.查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )
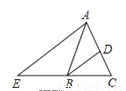
A. 40° B. 45° C. 60° D. 70°
A 【解析】根据平行线的性质可得∠CBD的度数,根据角平分线的性质可得∠CBA的度数,根据等腰三角形的性质可得∠C的度数,根据三角形内角和定理可得∠BAC的度数. 【解析】 ∵AE∥BD,∴∠CBD=∠E=35°,∵BD平分∠ABC,∴∠CBA=70°,∵AB=AC, ∴∠C=∠CBA=70°,∴∠BAC=180°﹣70°×2=40°. 故选A. “点睛”考查了平行...查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,点D、E是等边△ABC的边BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD于Q,已知PE=1,PQ=3,则AD等于( )
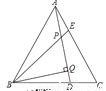
A. 5 B. 6 C. 7 D. 8
C 【解析】试题分析:∵△ABC是等边三角形,∴AB=AC,∠BAC=∠C=60°,又AE=CD, ∴△ABE≌△CAD(SAS), ∴∠ABE=∠CAD, ∴∠BPD=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°,∵BQ⊥AD,∴∠PBQ=30°, ∴BP=2PQ=2×3=6,∴AD=BE=BP+PE=6+1=7.故选C.查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,已知DE∥BC, AB∥CD,E为AB的中点,∠A=∠B.下列结论:①CD=AE;②AC=DE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的是( )
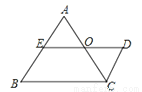
A. ①②④ B. ①③⑤ C. ②③④ D. ②④⑤
A 【解析】试题分析:∵已知DE∥BC,AB∥CD,∴四边形BCDE为平行四边形,∴CB=DE; ∵∠A=∠B,∴AC=BC, ∴AC=DE,即可得②正确; 根据平行线等分线段性质可得AO=CO,∵AB∥CD,∴∠A=∠DCO, 又∵∠AOE=∠COD, ∴△AOE≌△COD(ASA), ∴AE=CD,即可得①正确; OE=OD,O点是DE的中点;即可得④正确;结论③...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com