
到三角形三顶点距离相等的点是( ),到三角形三边距离相等的点是( )
A. 三条角平分线的交点,三条垂直平分线的交点
B. 三条角平分线的交点,三条中线的交点
C. 三条垂直平分线的交点,三条中线的交点
D. 三条垂直平分线的交点,三条角平分线的交点
D 【解析】试题分析:到三角形三个顶点矩形相等的点在三条中垂线的交点处,到三角形三边距离相等的点在三条角平分线的交点处.故选D. 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:解答题
先化简:(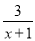 ﹣x+1)÷
﹣x+1)÷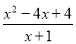 ,然后从﹣1≤x≤2中选一个合适的整数作为x的值代入求值.
,然后从﹣1≤x≤2中选一个合适的整数作为x的值代入求值.
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:单选题
在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如表:这些运动员跳高成绩的中位数和众数分别是( )
跳高成绩(m) | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 | 1.75 |
跳高人数 | 1 | 3 | 2 | 3 | 5 | 1 |
A. 1.65,1.70 B. 1.70,1.65 C. 1.70,1.70 D. 3,5
A 【解析】试题解析:跳高成绩为170的人数最多,故跳高成绩的众数为170; 共15名学生,中位数落在第8名学生处,第8名学生的跳高成绩为165,故中位数为165; 故选A.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题好拿分 题型:解答题
△ABC的三边满足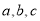 满足
满足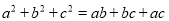 ,判断△ABC的形状并加以说明。
,判断△ABC的形状并加以说明。
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,已知DE∥BC, AB∥CD,E为AB的中点,∠A=∠B.下列结论:①CD=AE;②AC=DE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的是( )
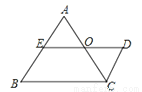
A. ①②④ B. ①③⑤ C. ②③④ D. ②④⑤
A 【解析】试题分析:∵已知DE∥BC,AB∥CD,∴四边形BCDE为平行四边形,∴CB=DE; ∵∠A=∠B,∴AC=BC, ∴AC=DE,即可得②正确; 根据平行线等分线段性质可得AO=CO,∵AB∥CD,∴∠A=∠DCO, 又∵∠AOE=∠COD, ∴△AOE≌△COD(ASA), ∴AE=CD,即可得①正确; OE=OD,O点是DE的中点;即可得④正确;结论③...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(三) 题型:填空题
如图,将矩形纸片ABCD沿AE折叠,使点B落在对角线AC上的点F处,再沿EG折叠,使点C落在矩形内的点H处,且E、F、H在同一直线上,若AB=6,BC=8,则CG的长是_____.
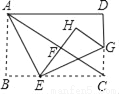
查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年八年级(上)期末复习测试数学试卷 题型:单选题
如图,△ABC中,∠ABC=90°,CE平分∠ACB,DE⊥AC,垂足为D,如果AB=3cm,那么AE+DE的值为( )
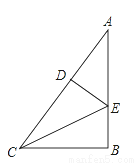
A. 2cm B. 4cm C. 5cm D. 3cm
D 【解析】试题分析:根据角平分线上的点到角两边的距离相等可得:DE=CE,则AE+DE=AE+CE=AC=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com