
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
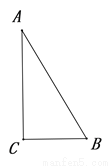
已知:如图,在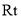 △
△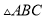 中,
中, 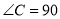 °,
°,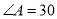 °.
°.
求证: 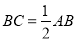 .
.
证明:
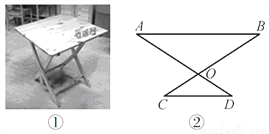
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得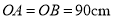 ,
, 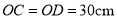 ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度 .
.
求:桌面与地面的高度.
查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
(2015成都)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
(1)120件;(2)150元. 【解析】试题分析:(1)设该商家购进的第一批衬衫是x件,则购进第二批这种衬衫可设为2x件,由已知可得,,这种衬衫贵10元,列出方程求解即可.(2)设每件衬衫的标价至少为a元,由(1)可得出第一批和第二批的进价,从而求出利润表达式,然后列不等式解答即可. 试题解析:(1)设该商家购进的第一批衬衫是件,则第二批衬衫是件. 由题意可得: ,解得,经检验...查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
在平面内,正方形ABCD与正方形CEFH如图放置,连接DE,BH,两线交于M,求证:
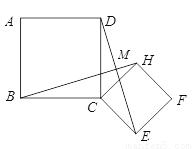
(1)BH=DE;
(2)BH⊥DE.
(1)证明见解析(2)证明见解析 【解析】试题分析:(1)根据正方形的性质可得BC=CD,CE=CH,∠BCD=∠ECH=90°,然后求出∠BCH=∠DCE,再利用“边角边”证明△BCH和△DCE全等,根据全等三角形对应边相等证明即可; (2)根据全等三角形对应角相等可得∠CBH=∠CDE,然后根据三角形的内角和定理求出∠DMB=∠BCD=90°,再根据垂直的定义证明即可. 试题...查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
观察下列等式:
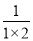 =1-
=1-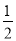 ,
, 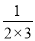 =
=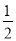 -
-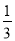 ,
, 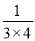 =
=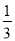 -
-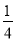 .
.
将以上三个等式的两边分别相加,得:
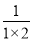 +
+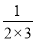 +
+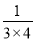 =1-
=1-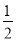 +
+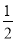 -
-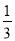 +
+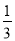 -
-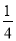 =1-
=1-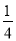 =
=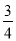 .
.
(1)直接写出计算结果:
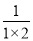 +
+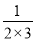 +
+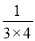 +…+
+…+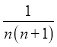 =________.
=________.
(2)仿照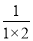 =1-
=1-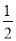 ,
, 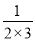 =
=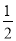 -
-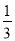 ,
, 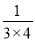 =
=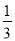 -
-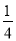 的形式,猜想并写出:
的形式,猜想并写出: 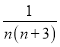 =________.
=________.
(3)解方程: 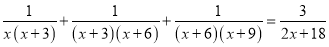 .
.
查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形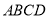 是“等对角四边形”,
是“等对角四边形”, 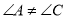 ,
, 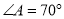 ,
, 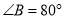 .求
.求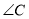 ,
, 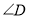 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
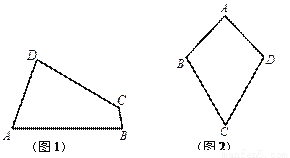
① 小红画了一个“等对角四边形”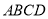 (如图2),其中
(如图2),其中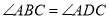 ,
, 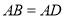 ,此时她发现
,此时她发现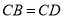 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”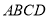 中,
中, 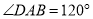 ,
, 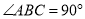 ,AB=AD=4,.求∠D和对角线
,AB=AD=4,.求∠D和对角线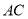 的长.
的长.
查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x2+ax+b),则:2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得:  ,解得:
,解得: 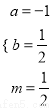 ,∴
,∴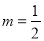 .
.
解法二:设2x3﹣x2+m=A•(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取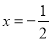 ,
, 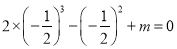 ,故
,故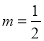 .
.
(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
m=﹣5,n=20. 【解析】试题分析: 仔细阅读题文中第(1)部分的内容,理解解题思想方法;然后参照(1)的方法:设x4+mx3+nx﹣16=A(x﹣1)(x﹣2),对x进行两次赋值,可得出两个关于m、n的方程,联立求解可得出m、n的值. 试题解析: 设x4+mx3+nx﹣16=A(x﹣1)(x﹣2)(A为整式),取x=1,得1+m+n﹣16=0①;取x=2,得16+8m...查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
观察下列方程的特征及其解的特点.
①x+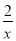 =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+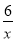 =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+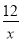 =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为____________,其解为x1=-4,x2=-5;
(2)根据这类方程特征,写出第n个方程为________________,其解为x1=-n,x2=-n-1;
(3)请利用(2)的结论,求关于x的方程x+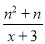 =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
图(1)是我们常见的“箭头图”,其中隐藏着哪些数学知识呢?下面请你解决以下问题:
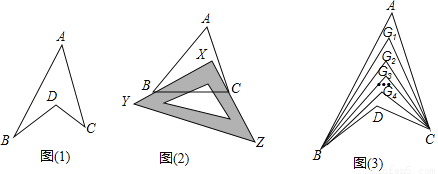
(1)观察如图(1)“箭头图”,试探究∠BDC与∠A、∠B、∠C之间大小的关系,并说明理由;
(2)请你直接利用以上结论,回答下列两个问题:
①如图(2),把一块三角板XYZ放置在△ABC上,使其两条直角边XY、XZ恰好经过点B、C.若∠A=50°,则∠ABX+∠ACX= ;
②如图(3),∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4,若∠BDC=135°,∠BG1C=67°,求∠A的度数.
(1)∠BDC=∠A+∠B+∠C(2)①40°②50° 【解析】试题分析:(1)连接AD并延长,根据三角形的外角和内角关系解答; (2)①利用(1)的结论,直接计算出∠ABX+∠ACX的度数; ②图(3)利用(1)的结论,根据∠BDC=135°,∠BG1C=67°,计算出相等的角:∠DBG4+∠DCG4的和,再次利用(1)的结论,求出∠A的度数. 试题解析:(1)∠BDC=...查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
【解析】
∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0∴m=﹣3,n=3
为什么要对2n2进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程..
解决问题:
(1)若x2﹣4xy+5y2+2y+1=0,求xy的值;
(2)已知a、b、c是△ABC的三边长,满足a2+b2=10a+12b﹣61,c是△ABC中最短边的边长,且c为整数,那么c可能是哪几个数?
(1);(2)c为2,3,4. 【解析】试题分析:(1)已知等式变形后,利用完全平方公式变形,利用非负数的性质求出x与y的值,即可求出xy的值; (2)由a2+b2=10a+12b-61,得a,b的值.进一步根据三角形一边边长大于另两边之差,小于它们之和,则b-a<c<a+b,即可得到答案. 试题解析:(1)∵x2﹣4xy+5y2+2y+1=0, ∴x2﹣4xy+4y2+y...查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
已知:方程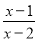 ﹣
﹣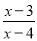 =
=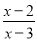 ﹣
﹣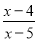 的解是x=
的解是x=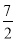 ,方程
,方程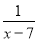 ﹣
﹣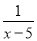 =
=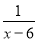 ﹣
﹣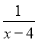 的解是x=
的解是x=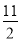 ,试猜想:
,试猜想:
(1)方程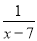 +
+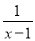 =
=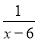 +
+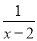 的解;
的解;
(2)方程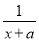 ﹣
﹣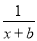 =
=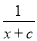 ﹣
﹣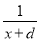 的解(a、b、c、d表示不同的数).
的解(a、b、c、d表示不同的数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com