
先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x2+ax+b),则:2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得:  ,解得:
,解得: 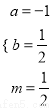 ,∴
,∴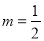 .
.
解法二:设2x3﹣x2+m=A•(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取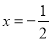 ,
, 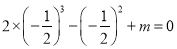 ,故
,故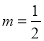 .
.
(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
m=﹣5,n=20. 【解析】试题分析: 仔细阅读题文中第(1)部分的内容,理解解题思想方法;然后参照(1)的方法:设x4+mx3+nx﹣16=A(x﹣1)(x﹣2),对x进行两次赋值,可得出两个关于m、n的方程,联立求解可得出m、n的值. 试题解析: 设x4+mx3+nx﹣16=A(x﹣1)(x﹣2)(A为整式),取x=1,得1+m+n﹣16=0①;取x=2,得16+8m...科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(C卷) 题型:单选题
下列说法:①若a为任意有理数,则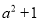 总是正数;②方程
总是正数;②方程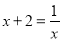 是一元一次方程;③若ab>0,a+b<0,则a<0,b<0;④
是一元一次方程;③若ab>0,a+b<0,则a<0,b<0;④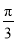 是分数;⑤单项式
是分数;⑤单项式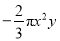 的系数是
的系数是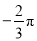 ,次数是4.其中错误的有( )
,次数是4.其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】根据乘方的意义,可知a2≥0,因此a2+1>0,是正数,故①正确; 根据一元一次方程是整式方程,故②不正确; 根据ab>0,可知a、b同号,再由a+b<0,可知a<0、b<0,故③正确; 由于是无理数,故④不正确; 单项式的系数是,故⑤正确. 故选C.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
分解因式:ax2﹣2a2x+a3=_____________ .
a(x﹣a)2 【解析】原式=a(x2﹣2ax+a2)=a(x﹣a)2.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:单选题
如图, 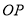 平分
平分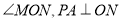 于点
于点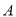 ,点
,点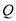 是射线
是射线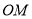 上的一个动点,若
上的一个动点,若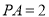 ,则
,则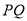 的最小值为( )
的最小值为( )
A. 1 B. 2 C. 3 D. 4
B 【解析】试题分析:根据题意点Q是射线OM上的一个动点,要求PQ的最小值,需要找出满足题意的点Q,根据直线外一点与直线上各点连接的所有线段中,垂线段最短,所以我们过点P作PQ垂直OM,此时的PQ最短,然后根据角平分线上的点到角两边的距离相等可得PA=PQ,利用已知的PA的值即可求出PQ的最小值. 【解析】 过点P作PQ⊥OM,垂足为Q,则PQ为最短距离, ∵OP平分∠MON,...查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:单选题
如图,我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下图中我国四大银行的商标图案中轴对称图形的是( )

A. ①②③ B. ②③④ C. ③④① D. ④①②
B 【解析】试题分析:根据轴对称图形的概念对各小题图形分析判断后利用排除法求解. 【解析】 ①不是轴对称图形, ②是轴对称图形, ③是轴对称图形, ④是轴对称图形, 综上所述,是轴对称图形的有②③④. 故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
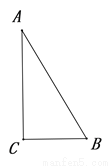
已知:如图,在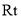 △
△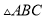 中,
中, 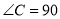 °,
°,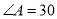 °.
°.
求证: 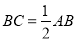 .
.
证明:
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得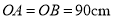 ,
, 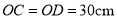 ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度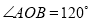 .
.
求:桌面与地面的高度.
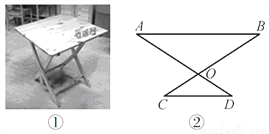
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
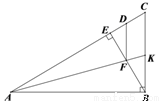
如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;
(2)求证:FD∥BC .
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:单选题
成都市为减少雾霾天气采取了多项措施,如对城区主干道进行绿化.现计划把某一段公路的一侧全部栽上银杏树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A. 5(x+21﹣1)=6(x﹣l) B. 5(x+21)=6(x﹣l) C. 5(x+21﹣1)=6x D. 5(x+21)=6x
A 【解析】【解析】 因为设原有树苗x棵,则路的长度为5(x+21﹣1)米,由题意,得 5(x+21﹣1)=6(x﹣1), 故选:A.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
若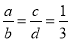 (b+d≠0),则
(b+d≠0),则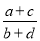 =________
=________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com