
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,在?ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.
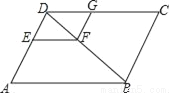
【答案】6
【解析】试题分析:根据平行线分线段成比例定理求出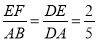 , 得到AB的长,根据平行四边形的性质求出CD,根据平行线分线段成比例定理得到比例式,计算即可.
, 得到AB的长,根据平行四边形的性质求出CD,根据平行线分线段成比例定理得到比例式,计算即可.
试题解析:∵EF∥AB,
∴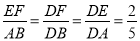 ,又EF=4,
,又EF=4,
∴AB=10,
∵四边形ABCD是平行四边形,
∴CD=AB=10,
∵FG∥ED,
∴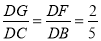 ,
,
∴DG=4,
∴CG=6.
【题型】解答题
【结束】
22
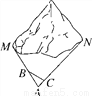
如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.
查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.
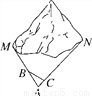
【答案】M、N两点之间的直线距离为1500米.
【解析】试题分析:先根据相似三角形的判定得出△ABC∽△AMN,再利用相似三角形的性质解答即可.
试题解析:在△ABC与△AMN中, 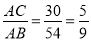 ,
, 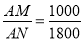 =
=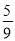 ,∴
,∴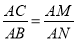 ,又∵∠A=∠A,
,又∵∠A=∠A,
∴△ABC∽△AMN,∴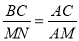 ,即
,即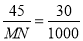 ,
,
解得:MN=1500米,
答:M、N两点之间的直线距离是1500米;
考点:相似三角形的应用.
【题型】解答题
【结束】
23
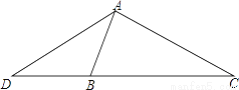
如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C, 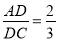 .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.
查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C, 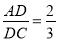 .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.
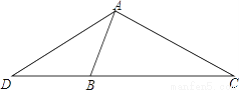
【答案】10
【解析】试题分析:根据相似三角形的判定定理得到△ADC∽△BAD,根据相似三角形的面积比等于相似比的平方即可得到结论.
试题解析:∵∠DAB=∠C,∠D=∠D, ∴△ADC∽△BAD,
∴ ,
,
∵△ADC的面积为18cm2 ,
∴△BDA的面积为8cm2 ,
∴△ABC的面积=△ADC的面积﹣△BDA的面积=10cm2
【题型】解答题
【结束】
24
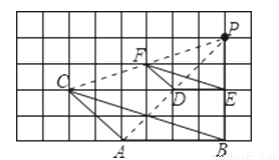
如图,在网格图中的△ABC与△DEF是否成位似图形?说明理由.如果是,同时指出它们的位似中心.
查看答案和解析>>
科目: 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,在网格图中的△ABC与△DEF是否成位似图形?说明理由.如果是,同时指出它们的位似中心.
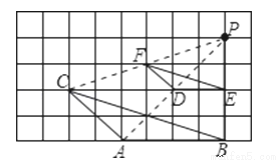
【答案】是位似图形,位似中心为P,理由见解析
【解析】试题分析:由题中的图形可以看出△ABC∽△DEF,进而又有位似中心,即可得其为位似图形.
试题解析:是位似图形,位似中心为P.
理由:∵AB∥DE,AC∥FD,
∴△ABC∽△DEF,
又其每组对应点所在的直线都经过同一个点P,
所以其为位似图形.
【题型】解答题
【结束】
25
如图①,直线y=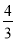 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
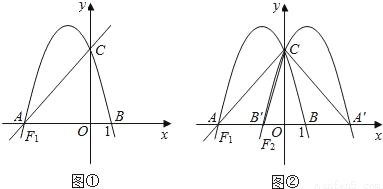
(1)求抛物线F1所表示的二次函数的表达式.
(2)若点M是抛物线F1位于第二象限图象上一点,求△AMC的面积最大时点M的坐标及S△AMC的最大值.
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)y=﹣x2﹣x+4; (2)当a=﹣时,S△AMC有最大值,最大值为9,此时,M(﹣,5); (3)当以A′、D、P为顶点的三角形与△AB′C相似时,点P的坐标为(2,0)或(﹣,0). 【解析】试题分析:(1)利用一次函数的解析式求出点A、C的坐标,然后再利用B点坐标即可求出二次函数的解析式;(2)由于M在抛物线F1上,所以可设M(a,﹣a2﹣a+4),然后分别计算S四边...查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
﹣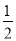 的相反数是( )
的相反数是( )
A. 2 B. 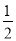 C. ﹣2 D. ﹣
C. ﹣2 D. ﹣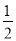
查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
下列计算正确的是( )
A. a3+a2=a5 B. a3•a2=a5 C. (a3)2=a9 D. a3﹣a2=a
B 【解析】试题解析:A. a3+a2≠a5,故原选项错误; B. a3•a2=a5,正确; C. (a3)2=a6,故原选项错误; D. a3﹣a2≠a,故原选项错误. 故选B.查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
圆柱的侧面展开图是( )
A. 等腰三角形 B. 等腰梯形 C. 扇形 D. 矩形
D 【解析】试题解析:圆柱的侧面展开图是矩形. 故选D.查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
已知两圆的半径分别为1和4,圆心距为3,则两圆的位置关系是( )
A. 外离 B. 外切 C. 相交 D. 内切
D 【解析】试题解析:∵两圆的半径分别为1和4,圆心距为3, 又∵R+r=1+4=5,R-r=4-1=3,圆心距d=R-r=3, ∴两圆的位置关系是内切. 故选D.查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
一只小鸟自由自在地在空中飞行,然后随意落在图中所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )

A. 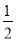 B.
B. 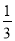 C.
C. 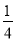 D.
D. 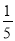
查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
如图所示的正四棱锥的俯视图是( )
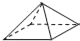
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com