一个零件的形状如图所示，工人师傅按规定做得∠B=90°，

AB＝3，BC＝4，CD＝12，AD＝13，假如这是一块钢板，你能帮工人师傅计算一下这块钢板的面积吗？

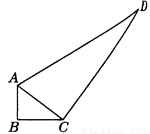
【答案】面积等于36

【解析】试题分析：利用勾股定理求AC,再利用勾股定理逆定理求∠ACB=90°，分别求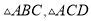的面积.

试题解析：

∠B=90°，AB＝3，BC＝4,AC=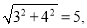

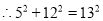=169,

所以∠ACD=90°,

.

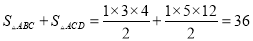所以面积是36.

【题型】解答题
【结束】
22

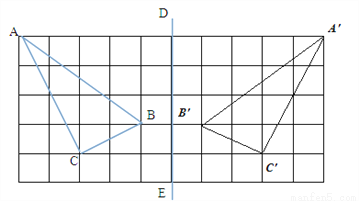
如图，在所给正方形网格（每个小网格的边长是1）图中完成下列各题.

（1）格点△ABC（顶点均在格点上）的面积=_________；

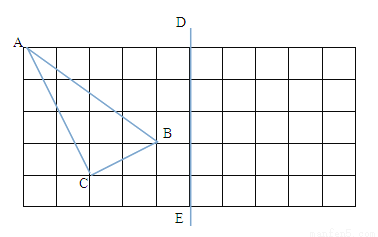
（2）画出格点△ABC关于直线DE对称的△A1B1C1；

（3）在DE上画出点P，使PB+PC最小，并求出这个最小值．

（1）面积等于5（2）图形见解析（3）最小值是根号17 【解析】试题分析：(1)利用勾股定理求出三角形边长，并证明是直角三角形求面积.(2)画出A，B，C的对称点A1,B2,C3，连接三角形.(3)利用对称利用两点之间直线最短求最小值. 试题解析： （1）分别利用勾股定理求得AC=2,AB=,BC=， ,所以∠ACB=90°，面积等于=5. （2）画出A，B，C的对称点A1...

如图，在所给正方形网格（每个小网格的边长是1）图中完成下列各题.

（1）格点△ABC（顶点均在格点上）的面积=_________；

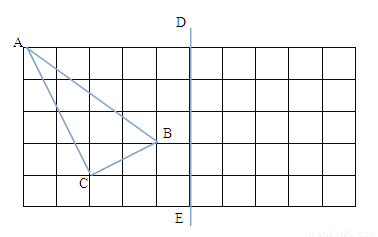
（2）画出格点△ABC关于直线DE对称的△A1B1C1；

（3）在DE上画出点P，使PB+PC最小，并求出这个最小值．

【答案】（1）面积等于5（2）图形见解析（3）最小值是根号17

【解析】试题分析：(1)利用勾股定理求出三角形边长，并证明是直角三角形求面积.(2)画出A，B，C的对称点A1,B2,C3，连接三角形.(3)利用对称利用两点之间直线最短求最小值.

试题解析：

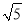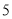（1）分别利用勾股定理求得AC=2,AB=,BC=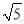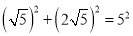， ,所以∠ACB=90°，面积等于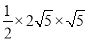=5.

（2）画出A，B，C的对称点A1,B2,C3，连接三角形.如下图.

（3）作B点对称B’,连接B’C交DE于P,B’P+PC=BP+CP,所以使PB+PC最小.

利用勾股定理B’C=，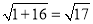

所以最小值是根号17.

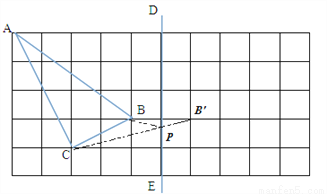
点睛：平面上最短路径问题

（1）归于“两点之间的连线中，线段最短”.凡属于求“变动的两线段之和的最小值”时，大都应用这一模型.

（2）归于“三角形两边之差小于第三边”.凡属于求“变动的两线段之差的最大值”时，大都应用这一模型.

（3）平面图形中，直线同侧两点到直线上一点距离之和最短问题.

【题型】解答题
【结束】
23

已知一次函数y＝kx＋7的图像经过点A（2，3）．

（1）求k的值；

（2）判断点B（－1，8），C（3，1）是否在这个函数的图像上，并说明理由；

（3）当－3＜x＜－1时，求y的取值范围．

（1）k=-2（2）点B不在，点C在，（3）9＜y＜13 【解析】 试题分析：（1）把点A（2，3）代入y＝kx＋7即可求出k的值；（2）点B（－1，8），C（3，1）的横坐标代入函数解析式验证即可；（3）根据x的取值范围，即可求出y的取值范围． 试题解析：（1）把点A（2，3）代入y＝kx＋7得：k=-2 （2）当x=-1时，y=-2×（-1）+7=9 ∵9≠8∴点...

已知一次函数y＝kx＋7的图像经过点A（2，3）．

（1）求k的值；

（2）判断点B（－1，8），C（3，1）是否在这个函数的图像上，并说明理由；

（3）当－3＜x＜－1时，求y的取值范围．

【答案】（1）k=-2（2）点B不在，点C在，（3）9＜y＜13

【解析】

试题分析：（1）把点A（2，3）代入y＝kx＋7即可求出k的值；（2）点B（－1，8），C（3，1）的横坐标代入函数解析式验证即可；（3）根据x的取值范围，即可求出y的取值范围．

试题解析：（1）把点A（2，3）代入y＝kx＋7得：k=-2

（2）当x=-1时，y=-2×（-1）+7=9

∵9≠8∴点B不在抛物线上．

当x=3时，y=-2×3+7=1

∴点C在抛物线上

（3）当x=-3时，y=13，当x=-,1时，y=9，所以9＜y＜13

考点：一次函数．

【题型】解答题
【结束】
24

顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地，甲出发0.5h后乙开始出发，结果比甲早1（h）到达B地，如图，线段OP、MN分别表示甲、乙两车离A地的距离S（km）与时间t（h）的关系，a表示A、B两地之间的距离．请结合图中的信息解决如下问题：

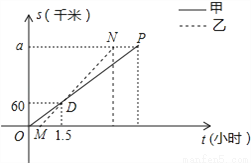
（1）分别计算甲、乙两车的速度及a的值；

（2）乙车到达B地后以原速立即返回，请问甲车到达B地后以多大的速度立即匀速返回，才能与乙车同时回到A地？并在图中画出甲、乙两车在返回过程中离A地的距离S（km）与时间t（h）的函数图象．

（1）甲、乙两车的速度分别为40km/h、60km/h，a的值是180km；（2）甲返回时的速度为90km/h 【解析】试题分析：（1）观察t轴，s轴表示的意义，利用v=求速度.(2) ，利用v=为等量列方程求解. 试题解析： （1）由图象得：甲的速度为：60÷1.5=40（km/h）， 乙的速度为：60÷（1.5﹣0.5）=60（km/h）， 求a的方法如下： ...

顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地，甲出发0.5h后乙开始出发，结果比甲早1（h）到达B地，如图，线段OP、MN分别表示甲、乙两车离A地的距离S（km）与时间t（h）的关系，a表示A、B两地之间的距离．请结合图中的信息解决如下问题：

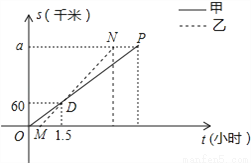
（1）分别计算甲、乙两车的速度及a的值；

（2）乙车到达B地后以原速立即返回，请问甲车到达B地后以多大的速度立即匀速返回，才能与乙车同时回到A地？并在图中画出甲、乙两车在返回过程中离A地的距离S（km）与时间t（h）的函数图象．

【答案】（1）甲、乙两车的速度分别为40km/h、60km/h，a的值是180km；（2）甲返回时的速度为90km/h

【解析】试题分析：（1）观察t轴，s轴表示的意义，利用v=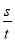求速度.(2) ，利用v=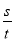为等量列方程求解.

试题解析：

（1）由图象得：甲的速度为：60÷1.5=40（km/h），

乙的速度为：60÷（1.5﹣0.5）=60（km/h），

求a的方法如下：

方法1：由题意得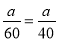： ﹣1﹣0.5，解得：a=180；

方法2：设甲到达B地的时间为t时，则乙所用的时间为（t﹣1﹣0.5）时，

由题意得：40t=60（t﹣1﹣0.5），

t=4.5，

∴a=40t=40×4.5=180，

答：甲、乙两车的速度分别为40km/h、60km/h，a的值是180km.

（2）方法1：设甲返回时的速度为xkm/h，

则,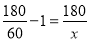

解得：x=90，

经检验：x=90是原方程的解，用符合题意，

所以，甲返回时的速度为90km/h；

方法2：甲、乙同时返回A地，则甲返回时所用的时间为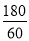： -1=2，

所以，甲返回时的速度为：180÷2=90（km/h）．

图象如图所示：

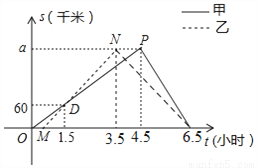
【题型】解答题
【结束】
25

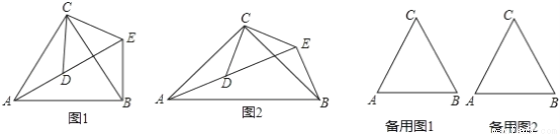
（1）问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE．

填空：① ∠AEB的度数为_______；②线段AD、BE之间的数量关系是______．

（2）拓展研究：

如图2，△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=90°，点A、D、E在同一直线上，若AE=15，DE=7，求AB的长度．

（3）探究发现：

图1中的△ACB和△DCE，在△DCE旋转过程中当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．

（1）60°．AD=BE；（2）AB=17；（3）∠AOE的度数是60°或120°． 【解析】试题分析：（1）由条件易证△ACD≌△BCE，从而得到：AD=BE，∠ADC=∠BEC．由点A，D，E在同一直线上可求出∠ADC，从而可以求出∠AEB的度数． （2）仿照（1）中的解法可求出∠AEB的度数，证出AD=BE；由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=...

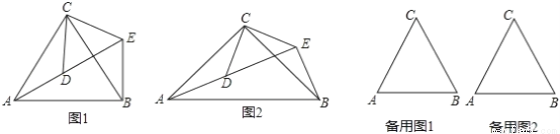
（1）问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE．

填空：① ∠AEB的度数为_______；②线段AD、BE之间的数量关系是______．

（2）拓展研究：

如图2，△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=90°，点A、D、E在同一直线上，若AE=15，DE=7，求AB的长度．

（3）探究发现：

图1中的△ACB和△DCE，在△DCE旋转过程中当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．

【答案】（1）60°．AD=BE；（2）AB=17；（3）∠AOE的度数是60°或120°．

【解析】试题分析：（1）由条件易证△ACD≌△BCE，从而得到：AD=BE，∠ADC=∠BEC．由点A，D，E在同一直线上可求出∠ADC，从而可以求出∠AEB的度数．

（2）仿照（1）中的解法可求出∠AEB的度数，证出AD=BE；由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME，从而证到AE=2CH+BE．

（3）由（1）知△ACD≌△BCE，得∠CAD=∠CBE，由∠CAB=∠ABC=60°，可知∠EAB+∠ABE=120°，根据三角形的内角和定理可知∠AOE=60°．

试题解析：（1）①∵△ACB和△DCE均为等边三角形，

∴CA=CB，CD=CE，∠ACB=∠DCE=60°.

∴∠ACD=∠BCE.

在△ACD和△BCE中，

，

∴△ACD≌△BCE(SAS).

∴∠ADC=∠BEC.

∵△DCE为等边三角形，

∴∠CDE=∠CED=60°.

∵点A，D，E在同一直线上，

∴∠ADC=120°.

∴∠BEC=120°.

∴∠AEB=∠BEC?∠CED=60°.

故答案为：60°.

②∵△ACD≌△BCE，

∴AD=BE.

故答案为：AD=BE.

（2）∵△ACB和△DCE均为等腰直角三角形，

∴CA=CB，CD=CE，∠ACB=∠DCE=90°.

∴∠ACD=∠BCE.

在△ACD和△BCE中，

，

∴△ACD≌△BCE(SAS).

∴AD=BE=AE-DE=8，∠ADC=∠BEC，

∵△DCE为等腰直角三角形，

∴∠CDE=∠CED=45°.

∵点A，D，E在同一直线上，

∴∠ADC=135°.

∴∠BEC=135°.

∴∠AEB=∠BEC?∠CED=90°.

∴AB=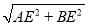=17；

（3）由（1）知△ACD≌△BCE，

∴∠CAD=∠CBE，

∵∠CAB=∠CBA=60°，

∴∠OAB+∠OBA=120°

∴∠AOE=180°?120°=60°，

同理求得∠AOB=60°，

∴∠AOE=120°，

∴∠AOE的度数是60°或120°.

点睛：本题考查了等边三角形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质等知识，考查了运用已有的知识和经验解决问题的能力.

【题型】解答题
【结束】
26

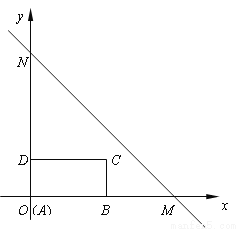
如图，直线MN：y＝－x＋b与x轴交于点M（4，0），与y轴交于点N，长方形ABCD的边AB在x轴上，AB＝2，AD＝1．长方形ABCD由点A与点O重合的位置开始，以每秒1个单位长度的速度沿x轴正方向作匀速直线运动，当点A与点M重合时停止运动．设长方形运动的时间为t秒，长方形ABCD与△OMN重合部分的面积为S．

（1）求直线MN的解析式；

（2）当t＝1时，请判断点C是否在直线MN上，并说明理由；

（3）请求出当t为何值时，点D在直线MN上；

（4）直接写出在整个运动过程中S与t的函数关系式

（1）y=-x+4（2）t=1时，点C（3，1）在直线MN上（3）t=3时，点D在直线MN上（4）S= 【解析】试题分析：（1）把点（4，0）代入直线即可求得结果； （2）先求出当=1时点A运动的路程，即可得到点C的坐标，再代入直线MN的解析式即可判断； （3）先得到运动开始时点D坐标，再令，得到此时点D的坐标即可判断； （4）分、、、四种情况分析即可. （1）∵直线...

将3x﹣7=2x变形正确的是（　　）

A. 3x+2x=7 B. 3x﹣2x=﹣7 C. 3x+2x=﹣7 D. 3x﹣2x=7

D 【解析】试题分析：根据选项特点，左边是未知项，右边是常数，所以等式两边都加上7，再减去2x． 【解析】 等式两边都加7得：3x=2x+7， 等式两边都减2x得：3x﹣2x=7． 故选D．

下列说法不正确的有（　　）个

①﹣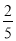πxy2的系数为﹣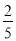；②1是单项式；③绝对值等于它本身的数是正数；④倒数等于它本身的数有±1；⑤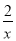﹣5是代数式；⑥单项式（﹣2）x2y3的次数为7．

A. 3 B. 4 C. 2 D. 1

A 【解析】试题解析：①﹣ πxy2的系数为故错误. ② 正确. ③绝对值等于它本身的数是非负数.故错误. ④ 正确. ⑤ 正确. ⑥ 次数是5.故错误. 有3个错误. 故选A.

如果3x2myn+1与﹣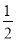x2ym+3是同类项，则m，n的值为（　　）

A. m=﹣1，n=3 B. m=1，n=3 C. m=﹣1，n=﹣3 D. m=1，n=﹣3

B 【解析】【解析】 ∵3x2myn+1与﹣x2ym+3是同类项，∴2m=2，n+1=m+3，解得m=1，n=3．故选B．

当x=﹣1，y=﹣2时，代数式x2﹣2y+1的值是（　　）

A. ﹣1 B. ﹣2 C. 6 D. 4

C 【解析】试题解析： 时 故选C.

下列去括号的结果中，正确的是（　　）

A. ﹣3（x﹣1）=﹣3x+3 B. ﹣3（x﹣1）=﹣3x﹣1

C. ﹣3（x﹣1）=﹣3x﹣3 D. ﹣3（x﹣1）=﹣3x+1

A 【解析】试题解析： A.正确. 故选A.