
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:填空题
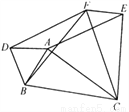
如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=__________.
查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
(本题满分6分)解分式方程: 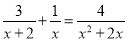
查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
先化简,再求值: 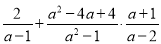 ,其中,a=
,其中,a=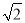 +1.
+1.
查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另行收费,甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
出租车的起步价是5元,超过3千米后,每千米的车费是1.5元. 【解析】试题分析:根据题意设出出租车的起步价为x元,超过3千米后每千米收费y元,根据甲的说法“我乘这种出租车走了11千米,付了17元”和乙的说法“我乘这种出租车走了23千米,付了35元”分别列方程,构成方程组求解即可. 试题解析:设出租车的起步价是x元,超过3千米后,每千米的车费是y元,由题意得: , 解得:, ...查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
2011年国家对“酒后驾车”加大了处罚力度,出台了不准酒后驾车的禁令.某记者在一停车场对开车的司机进行了相关的调查,本次调查结果有四种情况:①偶尔喝点酒后开车;②已戒酒或从来不喝酒;③喝酒后不开车或请专业司机代驾;④平时喝酒,但开车当天不喝酒.将这次调查情况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题.
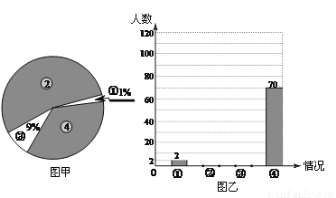
(1)该记者本次一共调查了 _____名司机.
(2)求图甲中④所在扇形的圆心角,并补全图乙.
(3)在本次调查中,记者随机采访其中的一名司机,求他属第②种情况的概率.
(4)请估计开车的10万名司机中,不违反“酒驾”禁令的人数.
【解析】 (1)2÷1%=200 (2)360°×=126°∴④所在扇形的圆心角为126° 200×9%=18(人) 200-18-2-70=110(人) 第②种情况110人,第③种情况18人. 注:补图②110人,③18人 (3)P(第②种情况)= ∴他是第②种情况的概率为 (4)10×(1-1%)=9.9(万人) 即:10万名开车的司...查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
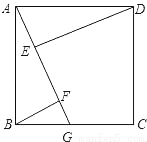
如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F.
求证:AF=BF+EF.
查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
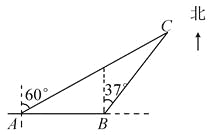
一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=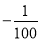 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳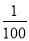 x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).
(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
(1)140;57500;(2)w内= x2+130x﹣62500,w外=x2+(150﹣a)x.(3)30. 【解析】 试题分析:(1)将x=1000代入函数关系式求得y,并根据等量关系“利润=销售额﹣成本﹣广告费”求得w内; (2)根据等量关系“利润=销售额﹣成本﹣广告费”“利润=销售额﹣成本﹣附加费”列出两个函数关系式; (3)对w内函数的函数关系式求得最大值,再求出...查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
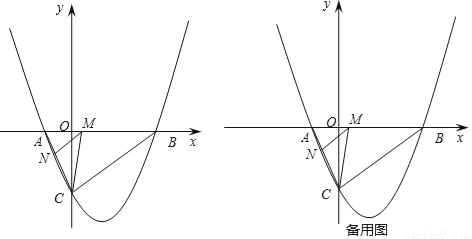
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2与y轴交于点C(0,4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.
(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连结CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
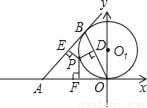
如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧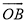 上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.
上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.
(1)求证:PD2=PE•PF;
(2)当∠BOP=30°,P点为OB的中点时,求D、E、F、P四个点的坐标及S△DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com