
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:填空题
分解因式:6ab﹣3a=_____.
3a(2b﹣1) 【解析】试题解析:6ab?3a=3a(2b?1). 故答案为:3a(2b?1).查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:填空题
a﹣2b+2=0,则代数式1+2b﹣a的值是_____.
3 【解析】试题解析:∵a?2b+2=0, ∴2b?a=2, ∴1+2b?a=1+2=3, 故答案为:3.查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:填空题
如图,F是平行四边形ABCD对角线BD上的点,BF:FD=1:3,则BE:EC=_____.
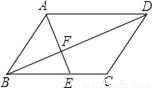
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:填空题
如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为_____.
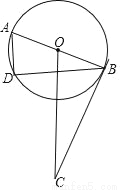
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:解答题
计算
(1)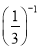 +16÷(﹣2)3+(2005﹣π)0﹣
+16÷(﹣2)3+(2005﹣π)0﹣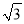 tan30°
tan30°
(2)(a﹣b)2+a(2b﹣a)
(1)1(2)b2 【解析】试题分析:(1)运用负整数指数幂,零指数幂,特殊角的三角函数,乘方运算等法则运算即可; (2)运用完全平方公式,单项式乘以多项式运算即可. 试题解析: 原式 原式查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:解答题
“五一”期间,某商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折(按售价的70%销售)和九折(按售价的90%销售),共付款386元,这两种商品原销售价之和为500元.问:这两种商品的原销售价分别为多少元?
甲、乙两种商品的原销售价分别为320元、180元 【解析】试题分析:用二元一次方程组解决问题的关键是找到2个合适的等量关系.设甲、乙两种商品的原销售价格分别为 元,根据两种商品原价为500元,可得方程(1),又根据两种商品打折后的总价为386元,又可得方程(2),由(1)(2)组成方程组,即可得到答案. 试题解析:设甲、乙两种商品的原销售价格分别为元, 依题意得 解得 ...查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:解答题
为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是多少?
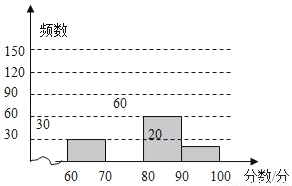
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:解答题
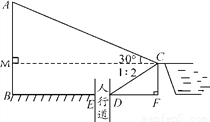
城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14 m的D处有一大坝,背水坡CD的坡度i=1∶2,坝高CF为2 m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2 m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域,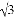 ≈1.732,
≈1.732,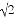 ≈1.414)
≈1.414)
查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:解答题
如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
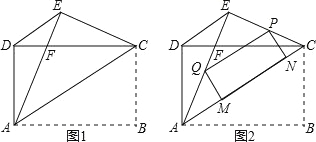
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
(1)证明见解析;(2)DF=.(3) PE=时,矩形PQMN的面积最大,最大面积为3. 【解析】试题分析:(1)由矩形和翻折的性质可知AD=CE,DC=EA,根据“SSS”可求得△DEC≌△EDA; (2)根据勾股定理即可求得. (3)由矩形PQMN的性质得PQ∥CA,所以,从而求得PQ,由PN∥EG,得出,求得PN,然后根据矩形的面积公式求得解析式,即可求得. 试题解析...查看答案和解析>>
科目: 来源:2017年海南省中考数学模拟试卷(三) 题型:解答题
如图所示,二次函数y=ax2﹣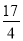 x+c的图象经过点A(0,1),B(﹣3,
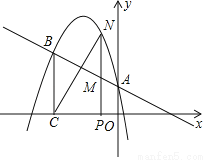
x+c的图象经过点A(0,1),B(﹣3, 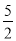 ),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
(1)求直线AB的解析式和二次函数的解析式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)点N是二次函数图象上一点(点N在AB上方),是否存在点N,使得BM与NC相互垂直平分?若存在,求出所有满足条件的N点的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com