
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
解方程:(1) (x+1)2-9=0 ;(2)(x-4)2+2(x-4)=0
(1);(2) 【解析】试题分析:(1)移项后利用直接开平方法解方程即可;(2)利用因式分解法解方程即可. 试题解析: (1) , ∴ , ∴ , (2)(x-4)(x-4+2)=0, ∴x-4=0,x-2=0, ∴x1=4,x2=2.查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
(1);(2)P(两次摸到红球)=. 【解析】试题分析:(1)根据4个小球中红球的个数,即可确定出从中任意摸出1个球,恰好摸到红球的概率; (2)列表得出所有等可能的情况数,找出两次都摸到红球的情况数,即可求出所求的概率. 试题解析:(1)4个小球中有2个红球, 则任意摸出1个球,恰好摸到红球的概率是; (2)列表如下: 红 红 ...查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E 求证:
(1)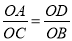 ;(2)
;(2)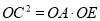
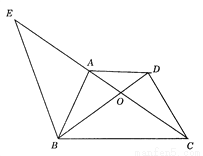
查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
为建设美丽家园,某企业逐年增加对环境保护的经费投入,2015年投入了400万元,到2017年投入了576万元.
(1)求2015年至2017年该单位环保经费投入的年平均增长率;
(2)该单位预计投入环保经费不低于700万元,若希望继续保持前两年的年平均增长率,问该目标能否实现?请通过计算说明理由.
(1)2015年至2017年该单位环保经费投入的年平均增长率为20%; (2)若希望继续保持前两年的年平均增长率,该目标不能实现. 【解析】试题分析: (1)设2015年至2017年该单位环保经费投入的年平均增长率为x,由题意得等量关系:2015年投入×(1+增长率)2=2017年投入,根据等量关系列出方程,再解即可; (2)利用2017年投入了576万元×(1+增长率),算出结...查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.求证:MN是⊙O的切线.
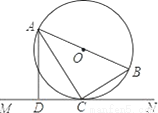
查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元(x为正整数),每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
(1)y=﹣10x2+90x+1900; (2)每件商品的售价定为61元或68元时,每天的利润恰为1980元; (3)每件商品的售价定为64元或65元时,每天可获得最大利润,最大利润是2100元. 【解析】试题分析:(1)利用销量乘以每件利润=总利润得出关系式即可; (2)利用(1)中所求关系式,进而使y=1980进而得出即可; (3)利用配方法求出二次函数最值,结合...查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
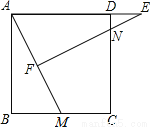
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
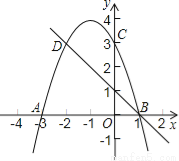
(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
(-2,3);y=--2x+3;-2<x<1. 【解析】试题分析:(1)根据抛物线的对称性来求点D的坐标; (2)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),把点A、B、C的坐标分别代入函数解析式,列出关于系数a、b、c的方程组,通过解方程组求得它们的值即可; (3)根据图象直接写出答案. 【解析】 (1)∵如图,二次函数的图象与x轴交于A(﹣3,...查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
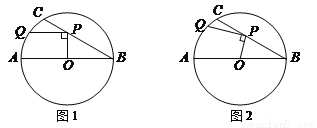
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
(1);(2). 【解析】试题分析:(1)在Rt△OPB中,由OP=OB·tan∠ABC可求得OP=,连接OQ,在Rt△OPQ中,根据勾股定理可得PQ的长;(2)由勾股定理可知OQ为定值,所以当当OP最小时,PQ最大.根据垂线段最短可知,当OP⊥BC时OP最小,所以在Rt△OPB中,由OP=OB·sin∠ABC求得OP的长;在Rt△OPQ中,根据勾股定理求得PQ的长. 试题解析:【解析...查看答案和解析>>
科目: 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
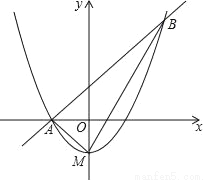
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com