
科目: 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
计算:|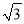 ﹣2|+20150﹣
﹣2|+20150﹣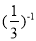 +3tan30°.
+3tan30°.
查看答案和解析>>
科目: 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
先化简,再求值:(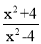 ﹣
﹣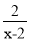 )
)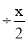 ,其中x=
,其中x=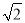 ﹣2.
﹣2.
查看答案和解析>>
科目: 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
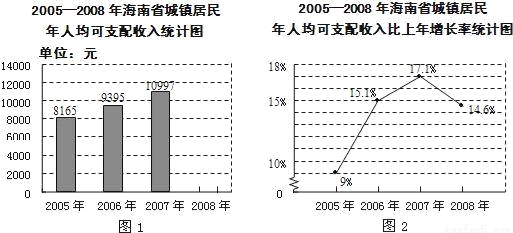
根据图1,图2所提供的信息,解答下列问题:
(1)2007年海南省城镇居民人均可支配收入为 元,比2006年增长 %;
(2)求2008年海南省城镇居民人均可支配收入(精确到1元),并补全条形统计图;
(3)根据图1指出:2005﹣2008年海南省城镇居民人均可支配收入逐年 (填“增加”或“减少”).
查看答案和解析>>
科目: 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
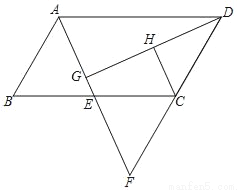
如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,并说明理由.
查看答案和解析>>
科目: 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据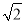 ≈1.41,
≈1.41,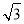 ≈1.73.
≈1.73.
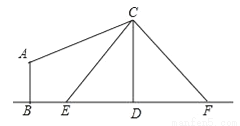
查看答案和解析>>
科目: 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
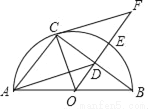
如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,点F为OE的延长线上一点且OC2=OD•OF.
(1)求证:CF为⊙O的切线.
(2)已知DE=2,tan∠BAC=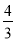 .
.
①求⊙O的半径;
②求sin∠BAD的值.
查看答案和解析>>
科目: 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
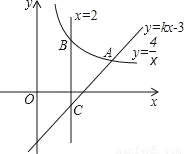
如图,反比例函数y=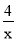 的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A,且点A的横坐标为4.
的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A,且点A的横坐标为4.
(1)求点A的坐标及一次函数的解析式;
(2)若直线x=2与反比例函数和一次函数的图象分别交于点B、C,求线段BC的长.
查看答案和解析>>
科目: 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
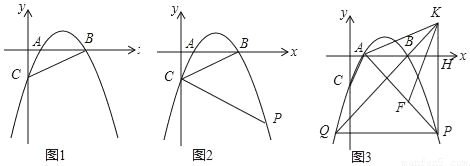
在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点且在直线BC下方,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4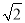 a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.
查看答案和解析>>
科目: 来源:重庆市秀山县2017-2018学年七年级上学期八校联考数学试卷 题型:单选题
-7的相反数是( )
A. -7 B. 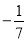 C.
C. 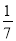 D. 7
D. 7
查看答案和解析>>
科目: 来源:重庆市秀山县2017-2018学年七年级上学期八校联考数学试卷 题型:单选题
在﹣22,(﹣2)2,﹣(﹣2),﹣|﹣2|中,负数的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题分析:根据有理数的乘方、正数和负数、绝对值的知识对各选项依次计算即可. 【解析】 ﹣22,=﹣4,(﹣2)2=4,﹣(﹣2)=2,﹣|﹣2|=﹣2, ∴是负数的有:﹣4,﹣2. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com