
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:填空题
若⊙O的半径为6cm,则⊙O中最长的弦为 ________厘米.
12 【解析】【解析】 ∵⊙O的半径为6cm,∴⊙O的直径为12cm,即圆中最长的弦长为12cm.故答案为:12.查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:填空题
如图,MN=3,以MN为直径的⊙O1 , 与一个半径为5的⊙O2相切于点M,正方形ABCD的顶点A,B在大圆上,小圆在正方形的外部且与CD切于点N,则正方形ABCD的边长为________ .
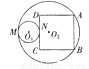
查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:填空题
请你写出一个二次函数,其图象满足条件:①开口向上;②与y轴的交点坐标为(0,1).此二次函数的解析式可以是________.
y=x2+1 【解析】试题解析:可取二次项系数为正数,常数项为正数,即可. 答案不唯一如:查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
公园里有一人设了个游戏摊位,游客只需掷一枚正方体骰子,如果出现3点,就可获得价值10元的奖品,每抛掷1次骰子只需付1元的费用.小明在摊位前观察了很久,记下了游客的中奖情况:
游客 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
抛掷次数 | 30 | 20 | 25 | 6 | 16 | 50 | 12 |
中奖次数 | 1 | 0 | 0 | 1 | 0 | 2 | 0 |
看了小明的记录,你有什么看法?
见解析. 【解析】试题分析:先根据正方体骰子的特点计算出3出现的概率,再与小明实际记录的中奖次数相比较即可得出结论. 试题解析:【解析】 对于一个普通的正方体骰子,3点出现的概率应为. 小明记录的抛掷次数为159次,中奖的次数应为27次左右,而实际中奖次数只有4次,于是可以怀疑摆摊人所用的骰子质量分布不均匀,要进一步证实这种怀疑,可以通过更多的试验来完成.查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为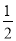 .
.
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.

查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.
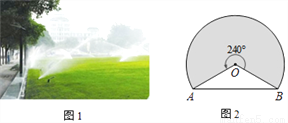
查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
在函数y=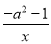 (a为常数),的图象上有三点(﹣3,y1),(﹣1,y2),(2,y3),试确定函数值y1 ,y2 ,y3的大小关系.
(a为常数),的图象上有三点(﹣3,y1),(﹣1,y2),(2,y3),试确定函数值y1 ,y2 ,y3的大小关系.
查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
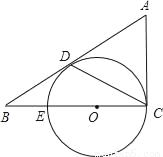
如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
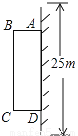
为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2 , 求y与x之间的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目: 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
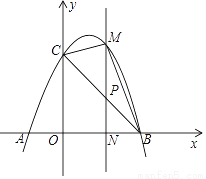
如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
(1)C(0,3),A(﹣1,0),B(3,0);(2)当t=时,△BCM的面积最大,此时P点坐标为( , );(3)Q点的坐标为(1, )或(1, )或(1, )或(1,﹣). 【解析】试题分析:(1)在抛物线解析式中,令x=0可求得C点坐标,令y=0则可求得A、B的坐标;(2)由B、C的坐标可求得直线BC的解析式为y=﹣x+3,可设P点坐标为(t,﹣t+3),则可表示出M点坐标,则可求得...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com