
һ�������Ŀڴ���װ�к졢�ơ���������ɫ������ɫ��ͬ�������ͬ�������к�����2����������1����������������1���Ǻ���ĸ���Ϊ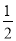 ��
��
��1�������������ĸ�����
��2����1�δӴ�����������1���Żأ�����2������������1�������û���״ͼ���б���ķ����������ζ���������ĸ��ʣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�꼪��ʡ�������п���ѧģ���Ծ� ���ͣ������
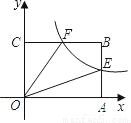
��ͼ����ƽ��ֱ������ϵ�У�����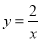 ��x��0����ͼ������OABC�ı�AB��BC���е�E��F�����ı���OEBF�����Ϊ_____��
��x��0����ͼ������OABC�ı�AB��BC���е�E��F�����ı���OEBF�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017���п���ѧ��ģ�Ծ� ���ͣ������
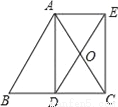
��ͼ��AD�ǵ�����ABC�ױ�BC�ϵĸߣ���O��AC�е㣬�ӳ�DO��E��ʹOE=OD������AE��CE��
��1����֤���ı���ADCE���Ǿ��Σ�
��2����AB=17��BC=16�����ı���ADCE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017���п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���CAB=65�㣬����ABC��ƽ�����Ƶ�A��ת����AB��C���λ�ã�ʹCC���AB������ת�ǵĶ���Ϊ��������
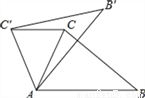
A. 35�� B. 40�� C. 50�� D. 65��
C �������������������CC���AB�� ���ACC��=��CAB=65�㣬 �ߡ�ABC�Ƶ�A��ת�õ���AB��C�䣬 ��AC=AC�䣬 ���CAC��=180��-2��ACC��=180��-2��75��=30�㣬 ���CAC��=��BAB��=30�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶����ĩģ����ѧ�Ծ� ���ͣ������
��ͼ����֪������y=��x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C������BC��
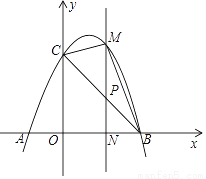
��1����A��B��C��������ꣻ
��2������PΪ�߶�BC��һ�㣨����B��C�غϣ���PM��y�ᣬ��PM���������ڵ�M����x���ڵ�N������BCM��������ʱ�����P�����ꣻ
��3���ڣ�2���������£�����BCM��������ʱ���������ߵĶԳ����ϴ���һ��Q��ʹ�á�CNQΪֱ�������Σ����Q�����꣮
��1��C��0��3����A����1��0����B��3��0������2����t=ʱ����BCM��������ʱP������Ϊ�� �� ������3��Q�������Ϊ��1�� ����1�� ����1�� ����1������. �������������������1���������߽���ʽ�У���x=0�����C�����꣬��y=0������A��B�����ꣻ��2����B��C����������ֱ��BC�Ľ���ʽΪy=��x+3������P������Ϊ��t����t+3������ɱ�ʾ��M�����꣬������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶����ĩģ����ѧ�Ծ� ���ͣ������
��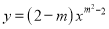 �Ƕ��κ�������m=________��
�Ƕ��κ�������m=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
Բ�ĵ���뾶Ϊ2��ĸ�߳�Ϊ4�������IJ����Ϊ��������
A. 8�� B. 16�� C. 4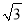 �� D. 4��
�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶��������ѧ�Ծ� ���ͣ������
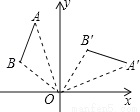
��ͼ�����߶�AB�Ƶ�O˳ʱ����ת90��õ��߶�A��B�䣬��ôA����2��5���Ķ�Ӧ��A���������_________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
ƽ���̳������ļס���������Ʒ��������Ʒÿ���ۼ�60Ԫ��������Ϊ50%��������Ʒÿ������50Ԫ���ۼ�80Ԫ
��1��������Ʒÿ������Ϊ_____Ԫ��ÿ��������Ʒ������Ϊ_____��
��2�������̳�ͬʱ�����ס���������Ʒ��50����ǡ���ܽ���Ϊ2100Ԫ����������Ʒ���ټ���
��3���ڡ�Ԫ�����ڼ䣬���̳�ֻ�Լ���������Ʒ�������µ��Żݴ������
����ǰһ���Թ����ܽ�� | �Żݴ�ʩ |
���ڵ���450Ԫ | ���Ż� |
����450Ԫ����������600Ԫ | ���ۼ۴���� |
����600Ԫ | ����600Ԫ���ְ˵�����Żݣ�����600Ԫ�IJ��ִ������Ż� |
�������Ż���������С��һ���Թ���������Ʒʵ�ʸ���504Ԫ����С���ڸ��̳�����������Ʒ���ټ���
40Ԫ/���� 60% ����������1����Ľ���Ϊx�����ݼ�������Ϊ50%�����x��ֵ�� ��2�����x�������ң�50-x�����������ܽ�����2100Ԫ���г�������⼴�ɣ� ��3��������������ۣ��ٴ���ǰ�������450Ԫ����������600Ԫ���ڴ���ǰ�������600Ԫ���ֱ��з�����⼴�ɣ� �������� ��1����Ľ���ΪxԪ/���� ��60��x����x=50%�� ...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com