如图，两个半径相等的直角扇形的圆心分别在对方的圆弧上，半径AE、CF交于点G，半径BE、CD交于点H，且点C是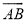的中点，若扇形的半径为2，则图中阴影部分的面积等于______．

2π﹣4 【解析】 两扇形的面积和为： , 过点C作CM⊥AE，作CN⊥BE，垂足分别为M、N， 则四边形EMCN是矩形， ∵点C是AB∧的中点， ∴EC平分∠AEB， ∴CM=CN， ∴矩形EMCN是正方形， ∵∠MCG+∠FCN=90°，∠NCB+∠FCN=90°， ∴∠MCG=∠NCH， ∴△CMG≌△CHN(ASA)， ...

解下列方程（1）(x－1)2－5＝0 ；（2） x2 －4x＝2．

(1) ； (2) 【解析】试题分析：本题考查了一元二次方程的解法.（1）移项后直接开平方即可；（2）先配方，即方程两边都加4，左边化为完全平方式，再开平方. 【解析】 （1）∵(x－1)2－5＝0 ； ∴(x－1)2=5， ∴x－1=±， ∴x=1±； （2）∵ x2 －4x＝2， ∴x2 －4x+4＝6， ∴(x－2)2=6， ∴x－2=...

用指定方法解下列方程 (1) 2x2 ＋5x－2＝0（用配方法）；(2) 9x2－(x－1)2＝0（用因式分解法）．

(1) ；(2) ； 【解析】试题分析：(1)方程两边除以2，将二次项系数化为1,常数项移到方程右边,然后左右两边都加上一次项系数一半的平方,左边化为完全平方式,右边合并为一个非负常数,开方转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;（2）把方程的左边利用平方差公式分解因式求解即可. 【解析】 (1) ∵2x2 ＋5x－2＝0， ∴ ， ∴， ∴ ，...

已知关于x的一元二次方程(a＋1)x2－x＋a2－2a－2＝0有一根是1，求a的值．

a＝2． 【解析】试题分析：将方程的根代入得到有关a的方程求解即可确定a的值，注意利用一元二次方程的定义舍去不合题意的根，从而确定a的值． 【解析】 将x=1代入， 得：（a+1）2﹣1+a2﹣2a﹣2=0， 解得：a1=﹣1，a2=2． ∵a+1≠0， ∴a≠﹣1， ∴a=2．

已知关于x的一元二次方程x2－6x＋a－2＝0．

（1）如果该方程有实数根，求实数a的取值范围；

（2）如果该方程有两个相等的实数根，求出这两个根．

(1) ；(2) 【解析】试题分析：（1）根据判别式的意义得到△=（-6）2-4（a-2）≥0，然后解不等式即可； （2）根据判别式的意义得到△=（-3）2-4（2a+1）=0，然后解关于a的方程得到a=5，则原方程变形为x2-4x+4=0，然后利用配方法解此一元二次方程． (1)根据题意得△=(?6)2?4(2a+1) ≥0， 解得a≤11； (2)根据题意得△=(...

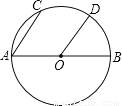
如图，已知AB是⊙O的直径，弦AC∥OD.

（1）求证： ．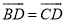

（2）若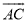的度数为58 º，求∠AOD的度数．

（1）证明见解析；（2）119°. 【解析】试题分析：(1)、连接OC，根据等腰三角形的性质得出∠OAC=∠ACO，根据平行线的性质得出∠OAC=∠BOD，∠DOC=∠ACO，从而得出∠BOD=∠COD，然后得出答案；(2)、根据弧AC的度数以及第一题的结论得出弧CD的度数，然后得出弧ACD的度数，从而求出圆心角的度数. 试题解析：(1)、连接OC．∵OA=OC，∴∠OAC=∠ACO．...

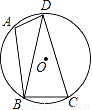
如图，已知四边形ABCD内接于圆O，∠A=105°，BD=CD．

（1）求∠DBC的度数；

（2）若⊙O的半径为3，求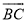的长．

（1）75°；（2）π． 【解析】试题分析：（1）根据圆内接四边形的性质可得∠C的度数，然后根据等边对等角可得答案； （2）首先计算出∠BDC的度数，再根据圆周角定理可得∠BOC的度数，进而可得的长． 【解析】 （1）∵四边形ABCD内接于圆O， ∴∠DCB+∠BAD=180°， ∵∠A=105°， ∴∠C=180°﹣105°=75°， ∵BD=CD， ...

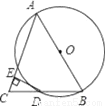
如图所示，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC于E．

（1）求证：AB=AC；

（2）求证：DE为⊙O的切线．

（1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）连接AD，根据中垂线定理不难求得AB=AC； （2）要证DE为⊙O的切线，只要证明∠ODE=90°即可． 试题解析：（1）连接AD； ∵AB是⊙O的直径， ∴∠ADB=90°． 又∵DC=BD， ∴AD是BC的中垂线． ∴AB=AC． （2）连接OD； ∵OA=OB，CD=BD...

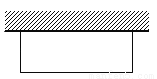
如图，学校准备修建一个面积为48 m2的矩形花园．它的一边靠墙，其余三边利用长20 m的围栏．已知墙长9 m，问围成矩形的长和宽各是多少?

围成矩形的长为8 m、宽为6 m． 【解析】试题分析：设宽为xm，则长为（20﹣2x）m，然后根据48平方米的长方形即可列出方程，解方程即可解决问题． 【解析】 设宽为x m，则长为（20﹣2x）m． 由题意，得 x•（20﹣2x）=48， 解得 x1=4，x2=6． 当x=4时，20﹣2×4=12＞9（舍去）， 当x=6时，20﹣2×6=8． 答：围成...

已知等腰三角形的两条边a,b是方程x2－kx＋12=0的两根，另一边c是方程x2－16=0的一个根, 求k的值.

或 【解析】试题分析：先解方程x2-16=0，得到c=4，再分两种情况进行讨论：①c=4是底边，那么a=b，由方程x2-kx+12=0的判别式△=0列出方程；②c=4是腰，那么将x=4代入x2-kx+12=0求出k的值. 【解析】 ∵c是方程x2?16=0的一个根， ∴c=4. 分两种情况： ①c=4是底边， 方程x2?kx+12=0的判别式△=k2?4×12...