
科目: 来源:湖北省元月联合测试数学试卷 题型:解答题
如图,△ABC内接于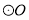 ,
, 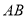 是
是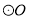 的直径,
的直径, 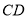 平分
平分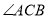 交
交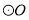 于点
于点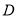 ,交
,交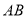 于
于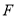 ,弦
,弦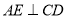 于点
于点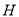 ,连接CE、OH.
,连接CE、OH.
(1)求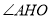 的度数;
的度数;
(2)若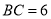 ,
, 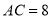 ,求
,求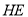 的长.
的长.

查看答案和解析>>
科目: 来源:湖北省元月联合测试数学试卷 题型:解答题
某商品现在售价为每件60元,每星期可卖出300件,市场调查反映:调整价格,每件涨价1元,每星期要少卖出10件;每件降价1元,每星期可多卖出20件.已知商品的进价为每件40元.
(1)设每件降价x元,每星期的销售利润为y元;
① 请写出y与x之间的函数关系式;
② 确定x的值,使利润最大,并求出最大利润;
(2)若涨价x元,则x= 元时,利润y的最大值为 元(直接写出答案,不必写过程).
(1)①②x=2或3时y最大为6120;(2)5, 6250 【解析】试题分析:(1)①设每件降价x元,每星期的销售利润为y元,根据等量关系“总利润=每件的利润×每星期的销售量”,写出函数关系式即可;②把函数的解析式化为顶点式,然后根据x取整数,即可求得最大利润;(2)表示出商品的周销售量,根据等量关系“总利润=每件的利润×每星期的销售量”,写出函数关系式,再根据二次函数的性质求出最大利润即...查看答案和解析>>
科目: 来源:湖北省元月联合测试数学试卷 题型:解答题
已知△ABC中, 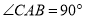 ,
, 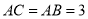 ,△CDE中,
,△CDE中, 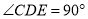 ,CD=DE=5,
,CD=DE=5,
连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若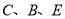 三点共线,
三点共线,  为
为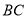 中点.
中点.
①直接指出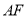 与
与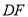 的关系______________;
的关系______________;
②直接指出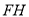 的长度______________;
的长度______________;
(2)将图(1)中的△CDE绕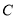 点逆时针旋转
点逆时针旋转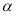 (如图2,
(如图2, 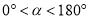 ),试确定
),试确定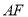 与
与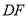 的关系,并说明理由;
的关系,并说明理由;
(3)在(2)中,若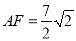 ,请直接指出点
,请直接指出点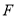 所经历的路径长.
所经历的路径长.
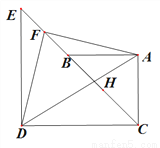
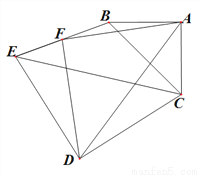
图1 图2
(1)①, ,②;(2), ,理由见解析;(3)或 【解析】试题分析:(1)①如图,过点F M⊥CD于M,FN⊥AC交CA的延长线于点N,根据已知条件易证四边形FMCN为正方形,可得FN=FM,再证△FNA≌△FMD,即可得∠NFA=∠DFM,DF=AF,所以∠NFA+∠AFM=∠DFM+∠AFM=∠DFA=90°,即可证得;②根据勾股定理求得BC=,EC=5 ,因为中点,F为BE的中点,可...查看答案和解析>>
科目: 来源:湖北省元月联合测试数学试卷 题型:解答题
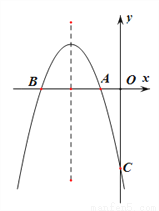
如图,已知抛物线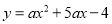 交
交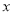 轴于点
轴于点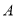 、点
、点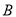 ,交
,交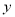 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求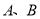 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点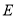 异于
异于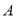 ,且
,且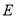 在对称轴右侧),直线
在对称轴右侧),直线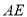 交对称轴于N,
交对称轴于N,
直线BE交对称轴于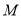 ,对称轴交
,对称轴交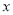 轴于
轴于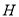 ,试确定
,试确定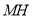 、
、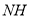 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目: 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
x=-1是方程x2+mx+1=0的一个实数根,则m的值是( )
A. 0 B. 1 C. 2 D. -2
C 【解析】试题分析:把x=﹣1代入方程x2+mx+1=0得:1﹣m+1=0, 解得:m=2, 故选C.查看答案和解析>>
科目: 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
下列四个图形中,属于中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
不透明袋子中有2个红球、3个绿球,这些球除颜色外其它无差别.从袋子中随机取出1个球,则( )
A. 能够事先确定取出球的颜色
B. 取到红球的可能性更大
C. 取到红球和取到绿球的可能性一样大
D. 取到绿球的可能性更大
D 【解析】试题分析:根据不同颜色的球的数量确定摸到哪种球的可能性的大小后即可确定正确的选项.∵不透明袋子中有2个红球、3个绿球,这些球除颜色外其它无差别,∴绿球数量大于红球数量,其摸球具有随机性, ∴摸到绿球的可能性大于摸到红球的可能性. 故选:D.查看答案和解析>>
科目: 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
已知点A(a,1)与点B(5,b)关于原点对称,则a、b值分别是( )
A. a=1,b=5 B. a=-5,b=-1
C. a=5,b=1 D. a=-1,b=-5
B 【解析】∵点A(a,1)与点B(5,b)关于原点对称, ∴a=-5,b=-1. 故选B.查看答案和解析>>
科目: 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,下列说法正确的是( )
A. 种植10棵幼树,结果一定是“有9棵幼树成活”
B. 种植100棵幼树,结果一定是“90棵幼树成活”和“10棵幼树不成活”
C. 种植10n棵幼树,恰好有“9n棵幼树成活”
D. 种植10n棵幼树,当n越来越大时,种植成活幼树的频率会越来越稳定于0.9
D 【解析】A. 种植10棵幼树,结果可能是“有9棵幼树成活”,故不正确; B. 种植100棵幼树,结果可能是“90棵幼树成活”和“10棵幼树不成活” ,故不正确; C. 种植10n棵幼树,可能有“9n棵幼树成活” ,故不正确; D. 种植10n棵幼树,当n越来越大时,种植成活幼树的频率会越来越稳定于0.9,故正确; 故选D.查看答案和解析>>
科目: 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
抛物线y=-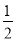 x2向左平移1个单位长度得到抛物线的解析式为( )
x2向左平移1个单位长度得到抛物线的解析式为( )
A. 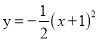 B.
B. 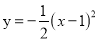
C. 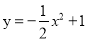 D.
D. 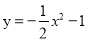
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com