
科目: 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
如图,AB=AE,∠B=∠AED,∠1=∠2.求证:△ABC≌△AED.
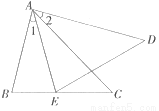
查看答案和解析>>
科目: 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
先化简,再求值: 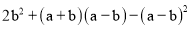 ,其中
,其中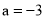 ,
, 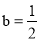 .
.
查看答案和解析>>
科目: 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
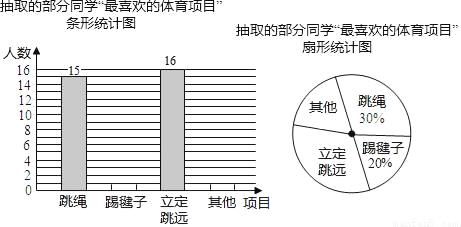
在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)小龙一共抽取了 名学生.
(2)补全条形统计图;
(3)求“其他”部分对应的扇形圆心角的度数.
查看答案和解析>>
科目: 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
甲、乙两辆汽车分别从A、B两城同时沿高速公路驶向C城.已知A、C两城的路程为500千米,B、C两城的路程为450千米,甲车比乙车的速度快10千米/时,结果两辆车同时到达C城,求两车的速度.
甲车的速度为100千米/时,乙车的速度为90千米/时. 【解析】试题分析:设甲的速度是x千米/时,那么乙的速度是(x-10)千米/时,路程知道,且同时到达,可以时间做为等量关系列方程求解. 试题解析:设乙车的速度为x千米/时,则甲车的速度为(x+10)千米/时. 根据题意,得. 解得x=90. 经检验,x=90是原方程的解,且符合题意. 当x=90时,x+10=...查看答案和解析>>
科目: 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
如图,在四边形ABCD中,∠BAD=∠B=∠C=90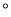 ,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
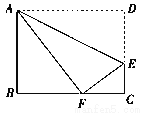
(1)求BF的长;
(2)求CE的长.
(1);(2) 【解析】试题分析:由折叠的性质可得:AF=AD=20,再由勾股定理可求出BF=12. (2)设CE=x,DE=EF=16-x,然后利用勾股定理得到,再解方程求出x即可. (1)∵△AFE是△ADE折叠得到的, ∴. 在Rt△ABE中, (2)∵△AFE是△ADE折叠得到的, ∴. 设,则 在Rt△EFC中, 即 解得...查看答案和解析>>
科目: 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
在△ABC中,∠BAC=90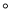 ,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使
,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使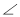 DAE=90
DAE=90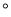 ,连结CE.
,连结CE.
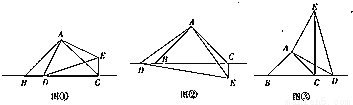
探究:如图①,当点D在线段BC上时,证明BC=CE+CD.
应用:在探究的条件下,若AB=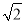 ,CD=1,则△DCE的周长为_______.
,CD=1,则△DCE的周长为_______.
拓展:(1)如图②,当点D在线段CB的延长线上时,BC、CD、CE之间的数量关系为_______.
(2)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为_______.
查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
分式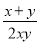 ,
, 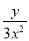 ,
, 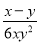 的最简公分母为( )
的最简公分母为( )
A. 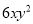 B.
B. 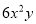 C.
C. 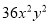 D.
D. 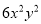
查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
已知x2﹣3x+1=0,则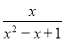 的值是( )
的值是( )
A. 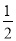 B. 2 C.
B. 2 C. 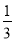 D. 3
D. 3
查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
如图,一圆柱高8cm,底面半径为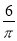 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
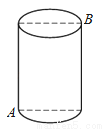
A. 12cm B. 10cm C. 8cm D. 6cm
B 【解析】底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为: ×2π×=6(cm),展开得: ∵BC=8cm,AC=6cm, 根据勾股定理得:AB==10(cm), 故选B.查看答案和解析>>
科目: 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
如图,下列条件中,不能证明△ABC≌△DCB的是( )
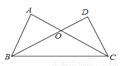
A. AB=DC,AC=DB B. AB=DC,∠ABC=∠DCB
C. BO=CO,∠A=∠D D. AB=DC,∠A=∠D
D 【解析】根据题意知,BC边为公共边. A.由“SSS”可以判定△ABC≌△DCB,故本选项错误; B.由“SAS”可以判定△ABC≌△DCB,故本选项错误; C.由BO=CO可以推知∠ACB=∠DBC,则由“AAS”可以判定△ABC≌△DCB,故本选项错误; D.由“SSA”不能判定△ABC≌△DCB,故本选项正确. 故选:D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com