
先化简,再求值: 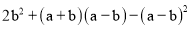 ,其中
,其中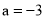 ,
, 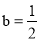 .
.
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:解答题
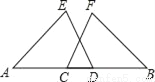
如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
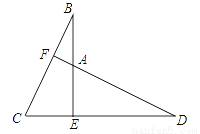
已知:如图,BE⊥CD,BE=DE,BC=DA.
求证:(1)△BEC≌△DAE;
(2)DF⊥BC.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:
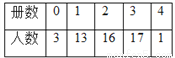
则这50名学生读数册数的众数、中位数是( )
A. 3,3 B. 3,2 C. 2,3 D. 2,2
B 【解析】∵这组样本数据中,3出现了17次,出现的次数最多, ∴这组数据的众数是3. ∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2,有=2, ∴这组数据的中位数为2; 故选B.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
分式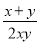 ,
, 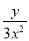 ,
, 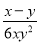 的最简公分母为( )
的最简公分母为( )
A. 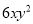 B.
B. 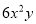 C.
C. 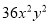 D.
D. 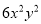
查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:填空题
如图,分别以线段BC的两个端点为圆心、适当长度(大于BC长的一半)为半径作圆弧,两弧相交于点D和E;作直线DE交BC于点F;在直线DE上任取一点A(点A不与点F重合),连结AB、AC.若AB=9cm,∠C=60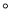 ,则CF的长为____cm.
,则CF的长为____cm.
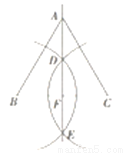
查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:单选题
如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
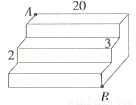
A. 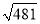 dm B. 20dm C. 25dm D. 35dm
dm B. 20dm C. 25dm D. 35dm
查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
已知二次函数y=ax2+bx+c(a≠0),其中a,b,c满足a+b+c=0和9a﹣3b+c=0,则该二次函数图象的对称轴是直线 .
x=﹣1. 【解析】 试题分析:解方程求出a,b的值,再根据对称轴公式即可求出该二次函数图象的对称轴. 【解析】 方程9a﹣3b+c=0减去方程a+b+c=0, 可得8a﹣4b=0, 根据对称轴公式整理得:对称轴为x==﹣1. 故该二次函数图象的对称轴是直线x=﹣1.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:解答题
已知抛物线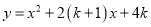 .
.
(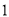 )求证:不论
)求证:不论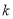 取何值,抛物线
取何值,抛物线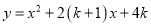 与
与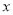 轴有交点.
轴有交点.
(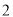 )若抛物线
)若抛物线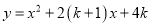 与
与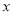 轴有两个交点,且这两个交点分别在直线
轴有两个交点,且这两个交点分别在直线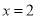 的两侧,求
的两侧,求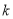 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com