
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
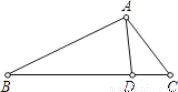
如图,若∠B=∠DAC,则△ABC∽_______,对应边的比例式是___________.
查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
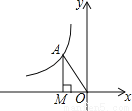
如图,若点A在反比例函数y=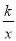 (k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k=_________________.
(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k=_________________.
查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
已知二次函数y=ax2+bx+c(a≠0),其中a,b,c满足a+b+c=0和9a﹣3b+c=0,则该二次函数图象的对称轴是直线 .
x=﹣1. 【解析】 试题分析:解方程求出a,b的值,再根据对称轴公式即可求出该二次函数图象的对称轴. 【解析】 方程9a﹣3b+c=0减去方程a+b+c=0, 可得8a﹣4b=0, 根据对称轴公式整理得:对称轴为x==﹣1. 故该二次函数图象的对称轴是直线x=﹣1.查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,DE∥BC,EF∥AB,且S△ADE=4,S△EFC=9,则△ABC的面积为
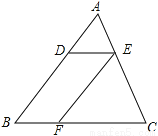
查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
计算:
(1)2sin 30°+cos 60°-tan 60°·tan 30°+cos245°.
(2)| 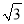 -5|+2·cos 30°+(
-5|+2·cos 30°+(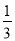 )-1+(9-
)-1+(9-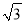 )0+
)0+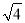
查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
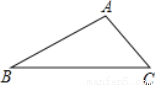
如图,△ABC是一仓库的屋顶的横截面,若∠B=30°,∠C=45°,AC=2,求线段AB的长.
查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
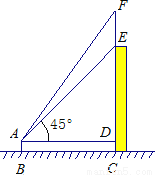
如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)
查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
(本小题10分)如图,已知A(-4,2)、B(n,-4)是一次函数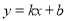 的图象与反比例函数
的图象与反比例函数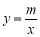 的图象的两个交点.
的图象的两个交点.
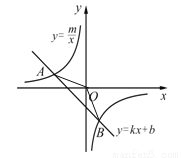
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
(1),;(2)或. 【解析】 试题分析:(1)先把A(﹣4,2)代入求出m=﹣8,从而确定反比例函数的解析式为;再把B(n,﹣4)代入求出n=2,确定B点坐标为(2,﹣4),然后利用待定系数法确定一次函数的解析式; (2)观察图象得到当或 时,一次函数的图象都在反比例函数图象的下方,即一次函数的值小于反比例函数的值. 试题解析:(1)把A(﹣4,2)代入得m=﹣4×2=﹣...查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
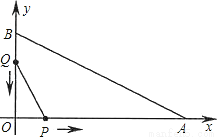
查看答案和解析>>
科目: 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,在△ABC中,∠CAB=120°,AD是∠CAB的平分线,AC=10,AB=8.
(1)求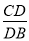 ;(2)求AD的长.
;(2)求AD的长.
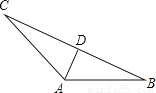
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com