
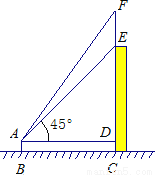
如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
4x2﹣3=12x(用公式法解).
, . 【解析】试题分析:把方程化为一般形式后再利用公式法解方程即可. 试题解析: 原方程整理为:4x2﹣12x﹣3=0, ∵a=4,b=﹣12,c=﹣3, ∴△=144﹣4×4×(﹣3)=192>0, 则x= = , ∴, .查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
在△ABC中,∠BAC=90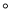 ,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使
,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使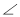 DAE=90
DAE=90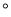 ,连结CE.
,连结CE.
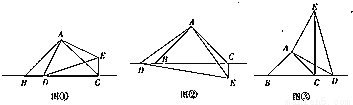
探究:如图①,当点D在线段BC上时,证明BC=CE+CD.
应用:在探究的条件下,若AB=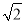 ,CD=1,则△DCE的周长为_______.
,CD=1,则△DCE的周长为_______.
拓展:(1)如图②,当点D在线段CB的延长线上时,BC、CD、CE之间的数量关系为_______.
(2)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为_______.
查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:单选题
若a+b=3,ab=2,则a2 +b2的值是( )
A. 2.5 B. 5 C. 10 D. 15
B 【解析】试题解析:∵a+b=3,ab=2, ∴a2+b2=(a+b)2-2ab=32-2×2=5. 故选B.查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
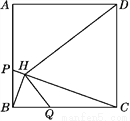
如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过点B作PC的垂线,垂足为点H,连接HD、HQ. (14分)
(1)图中有________对相似三角形;
(2)若正方形ABCD的边长为1,P为AB的三等分点,求△BHQ的面积;
(3)求证:DH⊥HQ.
查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
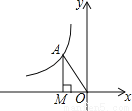
如图,若点A在反比例函数y=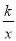 (k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k=_________________.
(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k=_________________.
查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,已知AB∥CD∥EF,那么下列结论正确的是( )
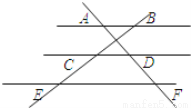
A. 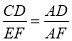 B.
B. 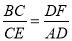 C.
C. 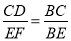 D.
D. 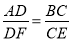
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的余弦值是______.
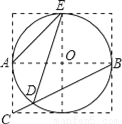
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:单选题
下列方程中是关于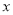 的一元二次方程的是( ).
的一元二次方程的是( ).
A. 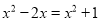 B.
B. 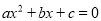
C. 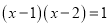 D.
D. 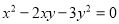
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com