对称轴与 y轴平行且经过原点O的抛物线也经过A（2，m），B（4，m），若△AOB的面积为4，则抛物线的解析式为________.

y =x2+3x或y =x2－3x 【解析】∵点A、B的坐标分别为：（2，m），B（4，m）， ∴AB=4-2=2，原点O到线段AB的距为： ， 又∵S△AOB=4， ∴，解得： ， ∴点A、B的坐标分别为：（2，4），B（4，4）或（2，-4），B（4，-4）. ∵抛物线过原点， ∴可设抛物线的解析式为， 现分以下两种情况讨论： （1）当点A...

解下列方程：

（1）x 2 ? 2 x = 2 x + 1

（2）2 x ( 2 ? x ) = 3 ( x ? 2 )

（1）x1=2+，x2=2-;（2）X1=2，x2=- 【解析】试题分析： （1）根据方程特点，本题用“配方法”或“公式法”解答即可； （2）根据方程特点，本题用“因式分解法”解答比较简单. 试题解析： （1）原方程可化为x2-4x=1， 配方得：x2-4x+4=5， ∴(x-2)2=5， ∴x-2=±， ∴x1=2+，x2=2-. （2...

如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．

（1）求证：△BCD≌△FCE；

（2）若EF∥CD，求∠BDC的度数．

详见解析. 【解析】试题分析：（1）、根据旋转图形的性质可得：CD=CE,∠DCE=90°，根据∠ACB=90°得出∠BCD=90°-∠ACD=∠FCE，结合已知条件得出三角形全等；（2）、根据全等得出∠BDC=∠E,∠BCD=∠FCE,从而得出∠DCE=90°，然后根据EF∥CD得出∠BDC=90°． 试题解析：（1）、∵将线段CD绕点C按顺时针方向旋转90°后得CE, ∴CD...

如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC 的三个顶点的坐标分别 A（-3，4）B（-5，2）C（-2，1）

（1）画出 △ABC关于y 轴的对称图形 △A1B1C1；

（2）画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ；

（3）求（2）中线段 OA扫过的图形面积．

（1）（2）见解析；（3）. 【解析】试题分析： （1）根据关于y轴对称的两个点，纵坐标相等，横坐标互为相反数即可点A1，B1，C1的坐标，根据坐标描出这三个点，再顺次连接即可； （2）连接AO，以AO为起始边，O为顶点，逆时针旋转90°，在终边上截取A2O=AO，A2即为A的旋转对应点；同理可得B2，C2，再顺次连接A2，B2，C2即可； （3）（2）中线段 O A 扫过...

如图，已知在△ABC中，∠A=90°

（1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作 图痕迹，不写作法和证明）．

（2）若∠B=60°，AB=3，求⊙P的面积．

（1）作图见解析；（2）3π． 【解析】试题分析：（1）与AB、BC两边都相切．根据角平分线的性质可知要作∠ABC的角平分线，角平分线与AC的交点就是点P的位置． （2）根据角平分线的性质和30°角的直角三角形的性质可求半径，然后求圆的面积． 试题解析：（1）如图所示，则⊙P为所求作的圆． （2）∵∠B=60°，BP平分∠ABC， ∴∠ABP=30°， ∴AP=，∴S...

甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式y=a（x﹣4）2+h，已知点O与球网的水平距离为5m，球网的高度为1.55m．

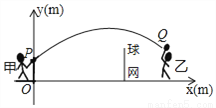
（1）当a=﹣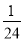时，①求h的值；②通过计算判断此球能否过网．

（2）若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为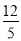m的Q处时，乙扣球成功，求a的值．

（1）①，②能；（2）－ 【解析】试题分析：（1）①将点P（0，1）代入即可求得h；②求出x=5时，y的值，与1.55比较即可得出判断； （2）将（0，1）、（7， ）代入代入即可求得a、h． （1）①当a=时， ，将点P（0，1）代入，得： ×16+h=1，解得：h=； ②把x=5代入，得： =1.625，∵1.625＞1.55，∴此球能过网； （2）把（0，1）、...

已知关于x的一元二次方程 x2-6x+m+4=0有两个实数根 x1，x2.

（1）求m的取值范围；

（2）若 x1，x2满足x2-2x1=-3 ，求m的值.

（1）m≤5;（2）m=5. 【解析】试题分析： （1）由原方程有两个实数根可知：根的判别式△，由此列出关于“m”的表达式，解不等式即可求得m的取值范围； （2）由方程 x2-6x+m+4=0有两个实数根 x1，x2可得：x1+x2=6，x1·x2=m+4，结合x2-2x1=-3即可解得m的值. 试题解析： （1）∵关于x的一元二次方程x2-6x+m+4 有实数根， ...

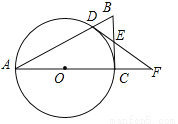
如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D，E为BC的中点，连接DE并延长交AC的延长线于点F．

（1）求证：DE是⊙O的切线；

（2）若CF=2，DF=4，求⊙O直径的长．

（1）证明见解析；（2）6． 【解析】试题分析：（1）连接OD、CD，由AC为⊙O的直径知△BCD是直角三角形，结合E为BC的中点知∠CDE=∠DCE，由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案； （2）设⊙O的半径为r，由OD2+DF2=OF2，即r2+42=（r+2）2可得r=3，即可得出答案． 试题解析：（1）如图，连接OD、CD．∵AC为⊙O的直径，∴△BC...

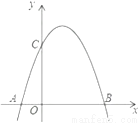
如图，是将抛物线y=-x2 平移后得到的抛物线，其对称轴为x=1，与x轴的一个交点为A(-1,0) ，另一交点为B，与y轴交点为C．

（1）求抛物线的函数表达式；

（2）若点N 为抛物线上一点，且BC⊥NC，求点N的坐标；

（3）点P是抛物线上一点，点Q是一次函数y=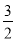x+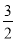的图象上一点，若四边形OAPQ为平行四边形，这样的点P、Q是否存在？若存在，分别求出点P、Q的坐标，若不存在，说明理由．

（1）y=-x2+2x+3；（2）（1，4）; （3）P、Q的坐标是(0,3)(1,3) 或,． 【解析】试题分析： （1）由题意可设该抛物线的解析式为，代入点（-1，0）求出k的值即可得到所求解析式； （2）由（1）中所得抛物线的解析式可求得点B、C的坐标，从而可求出直线BC的解析式，由直线NC⊥BC且过点C可求得NC的解析式，把NC的解析式和抛物线的解析式联立得到方程组，解方...

下列图形中是中心对称图形的有(　　)个．

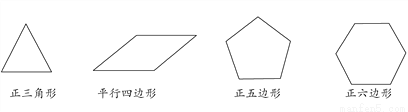
A. 1 B. 2 C. 3 D. 4

B 【解析】∵正三角形是轴对称能图形；平行四边形是中心对称图形；正五边形是轴对称图形；正六边形既是中心对称图形又是轴对称图形， ∴中心对称图形的有2个． 故选B.