
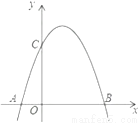
如图,是将抛物线y=-x2 平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0) ,另一交点为B,与y轴交点为C.
(1)求抛物线的函数表达式;
(2)若点N 为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=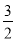 x+
x+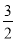 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源:广东省2017-2018学年八年级上学期第二次统测数学试卷 题型:解答题
计算:(a-b)(a+b)+2ab3÷ab
【解析】试题分析:按运算顺序先利用平方差公式进行乘法运算,同时进行后面的除法运算,然后再合并同类项即可. 试题解析:原式==.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:单选题
下列分式是最简分式的是( )
A.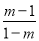 B.
B.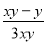 C.
C.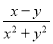 D.
D.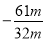
查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:填空题
在平面直角坐标系中,点P(1,-5)关于原点对称点P′的坐标是。
(-1,5). 【解析】 试题分析:点P(1,-5)关于原点对称的点的坐标是(-1,5).故答案为:(-1,5).查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:单选题
下列事件中是必然事件的是
A、实心铁球投入水中会沉入水底
B、抛出一枚硬币,落地后正面向上
C、明天太阳从西边升起
D、NBA篮球队员在罚球线投篮2次,至少投中一次
A 【解析】 试题分析:A、实心铁球投入水中会沉入水底是必然事件,故正确;B、抛出一枚硬币,落地后正面向上是随机事件,故错误;C、明天太阳从西边升起是不可能事件,故错误;D、NBA篮球队员在罚球线投篮2次,至少投中一次是随机事件,故错误.故选A.查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:解答题
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.

查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
二次函数y=ax2+bx+c(a≠0)的图象如图所示对称轴为直线x=-1,下列四个结论中:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
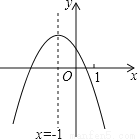
A. 4个 B. 3个 C. 2个 D. 1个
B 【解析】试题解析:∵抛物线和x轴有两个交点, ∴b2-4ac>0, ∴4ac-b2<0,∴①正确; ∵对称轴是直线x=-1,和x轴的一个交点在点(0,0)和点(1,0)之间, ∴抛物线和x轴的另一个交点在(-3,0)和(-2,0)之间, ∴把(-2,0)代入抛物线得:y=4a-2b+c>0, ∴4a+c>2b,∴②错误; ∵把x=1代入抛物线得:...查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
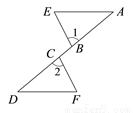
如图,A,B,C,D是同一条直线上的点,AC=BD,AE∥DF,∠1=∠2.求证:BE = CF.
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
等腰三角形的一个角是70°,它的底角的大小为( )
A. 70° B. 40° C. 70°或40° D. 70°或55°
D 【解析】若70°为顶角,则此等腰三角形的底角是(180°-70°)÷2=55°; 若70°为底角,则此等腰三角形的底角为70°, 综上,此等腰三角形的底角为70°或55°, 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com