
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:填空题
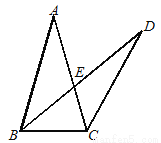
如图,在△ABC中,AB=AC=6,∠A=2∠BDC, BD交AC边于点E,且AE=4,则BE·DE=____________.
查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
计算: 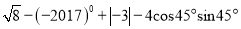
查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
计算: 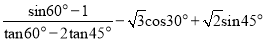 .
.
查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
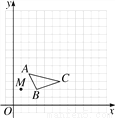
在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.
查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1、P2、P3、P4、P5是△DEF边上的5个格点,请按要求完成下列各题:
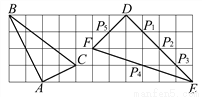
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)直接写出一个与△ABC相似的三角形,使它的三个顶点为P1、P2、P3、P4、P5中的三个格点.
(1)证明见解析(2)证明见解析(3)△P2P4P5 【解析】试题分析:(1)运用勾股定理可以得到各边的长,通过勾股定理的逆定理来证明是直角三角形. (2)根据勾股定理求出△ABC和△DEF的各边长,然后根据“三边对应成比例的两个三角形相似”说明即可; (3)根据△ABC的三边关系,求出点P2,P4,P5所形成三角形的三边长,根据“三边对应成比例的两个三角形相似”解答即可, ...查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
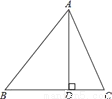
如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=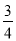 ,求sinC的值.
,求sinC的值.
查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
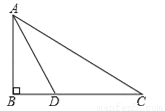
如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)
查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
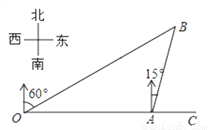
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).
查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
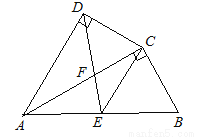
如图四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1) 求证:AC2=AB•AD;
(2) 求证:CE∥AD;
(3) 若AD=8,AB=12,求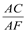 的值.
的值.
查看答案和解析>>
科目: 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
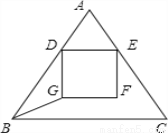
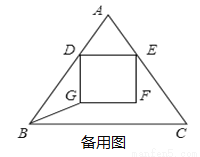
如图,在等腰△ABC中,点D、E分别是边AB、AC上的两点(点D不与点A、 点B重合),且DE∥BC,以DE为一边,在四边形DBCE的内部作正方形DEFG,已知AB=AC=5,BC=6.
(1)试求△ABC的面积;
(2)当GF与BC重合时,求正方形DEFG的边长;
(3)若BG的长度等于正方形DEFG的边长,试求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com