
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:填空题
一组数据2,3,x,5,7的平均数是5,则这组数据的中位数是_____.
5 【解析】试题分析:根据平均数的定义可得:(2+3+x+5+7)÷5=5,解得:x=8,则这组数据为:2、3、5、7、8,即这组数据的中位数是5.查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:填空题
直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
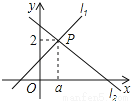
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:填空题
将一根24 cm的筷子,置于底面直径为15 cm,高8 cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为h cm,则h的取值范围是___________.
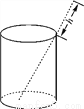
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:填空题
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y﹣4)2的值为 .
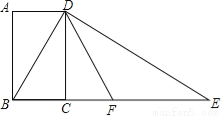
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:填空题
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn顶点Bn的横坐标为________________.
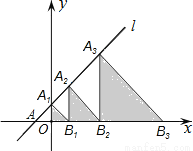
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:解答题
(1) 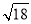 -
-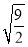 -
-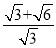 +(
+(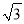 -2)0+
-2)0+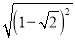 ;
;
(2)已知x=2+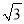 ,y=2-
,y=2-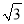 ,求代数式(
,求代数式(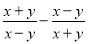 )·(
)·(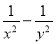 )的值.
)的值.
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:解答题
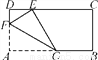
已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.如果折痕FG分别与AD,AB交于点F,G(如图),AF=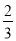 ,求DE的长.
,求DE的长.
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:解答题
永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数解析式预测该水库今年4月6日的水位;
(3)你能用求出的函数解析式预测该水库今年12月1日的水位吗?
(1)y=0.5x+5;(2)22.5米;(3)不能 【解析】试题分析:(1)先判断是一次函数,再用待定系数法求得解析式;(2)把x=6代入(1)中求得的解析计算即可;(3)不能,因为用所建立的函数模型远离已知数据作预测是不可靠的. 试题解析:(1)水库水位y随日期x的变化是均匀的,因此水库水位y与日期x之间是一次函数关系.设y=kx+b,把x=1,y=20.00和x=2,y=20.5...查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:解答题
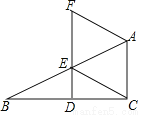
如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com