
科目: 来源:山东省济南市2018届九年级1月月考数学试卷 题型:解答题
随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少?

查看答案和解析>>
科目: 来源:山东省济南市2018届九年级1月月考数学试卷 题型:解答题
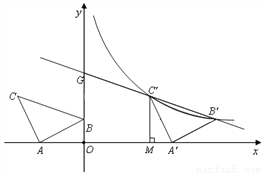
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0, d)、C(-3,2).
(1)求d的值;
(2)将△ABC沿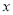 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
(3)在(2)的条件下,直线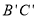 交y轴于点G,作
交y轴于点G,作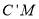 ⊥
⊥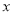 轴于
轴于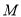 .
. 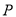 是线段
是线段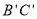 上的一点,若△
上的一点,若△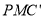 和△
和△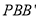 面积相等,求点
面积相等,求点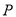 坐标.
坐标.
查看答案和解析>>
科目: 来源:山东省济南市2018届九年级1月月考数学试卷 题型:解答题
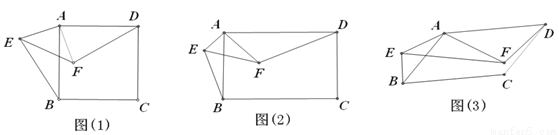
如图所示,(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°, 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=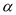 ,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用
,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用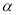 表示出直线BE、DF形成的锐角
表示出直线BE、DF形成的锐角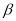 .
.
查看答案和解析>>
科目: 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
下面图案中是轴对称图形的有( )

A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】第1,2个图形沿某条直线折叠后直线两旁的部分能够完全重合,是轴对称图形, 故轴对称图形一共有2个。 故选:B.查看答案和解析>>
科目: 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
在△ABC中,∠A=70°,∠B=55°,则△ABC是( )
A. 钝角三角形 B. 等腰三角形
C. 等边三角形 D. 等腰直角三角形
B 【解析】【解析】 ∵在△ABC中,∠A=70°,∠B=55°,∴∠C=180°﹣∠A﹣∠B=55°,∴∠B=∠C,∴△ABC是等腰三角形.故选B.查看答案和解析>>
科目: 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
在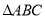 和
和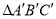 中,
中, 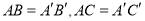 ,高
,高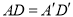 ,则
,则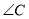 和
和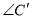 的关系是( )
的关系是( )
A. 相等 B. 互补
C. 相等或互补 D. 以上都不对
C 【解析】试题解析:当∠C′为锐角时,如图1所示, ∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′, ∴Rt△ADC≌Rt△A′D′C′, ∴∠C=∠C′; 当∠C为钝角时,如图3所示, ∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′, ∴Rt△ACD≌Rt△A′C′D′, ∴∠C=∠A′C′D′, ∴∠C+∠A′C′B′=180...查看答案和解析>>
科目: 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
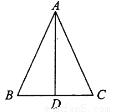
如图,在△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
A. 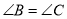 B.
B. 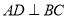 C.
C. 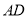 平分
平分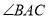 D.
D. 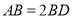
查看答案和解析>>
科目: 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
由下列条件不能判定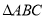 为直角三角形的是( )
为直角三角形的是( )
A. 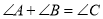 B.
B. 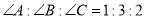
C. 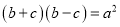 D.
D. 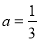 ,
, 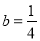 ,
, 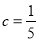
查看答案和解析>>
科目: 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
在一个直角三角形中,若斜边的长是13,一条直角边的长为12,那么这个直角三角形的面积是( )
A. 30 B. 40 C. 50 D. 60
A 【解析】试题解析:另一直角边长是: =5.则直角三角形的面积是×12×5=30. 故选A.查看答案和解析>>
科目: 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
下列说法中正确的是( )
A. 两个直角三角形全等 B. 两个等腰三角形全等
C. 两个等边三角形全等 D. 两条直角边对应相等的直角三角形全等
D 【解析】试题解析:A、两个直角三角形只能说明有一个直角相等,其他条件不明确,所以不一定全等,故本选项错误; B、两个等腰三角形,腰不一定相等,夹角也不一定相等,所以不一定全等,故本选项错误; C、两个等边三角形,边长不一定相等,所以不一定全等,故本选项错误; D、它们的夹角是直角相等,可以根据边角边定理判定全等,正确. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com