
科目: 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,
(1)每轮感染中平均一台电脑会感染几台电脑?
(2)若该病毒得不到有效控制,第3轮感染后,被感染的电脑会不会超过700台?说明理由
8台;会超过700台. 【解析】试题分析:(1)设每轮感染中平均一台电脑会感染台电脑,根据题意列出方程,求出方程的解即可; (2)求出3轮感染后被感染的电脑台数,再比较大小即可. 试题解析:(1)设每轮感染中平均一台电脑会感染台电脑,则依题意得: 整理得: 解得: (不合题意,舍)∴; (2)3轮感染后,被感染的电脑有查看答案和解析>>
科目: 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
如图,电信部门要在S区修建一座电视信号发射塔。按照设计要求,发射塔到两个城镇A,B距离必须相等,到两条高速公路m和n的距离也必须相等。发射塔应修建在什么位置?利用尺规作图标出它的位置。(不写作法,保留作图痕迹)
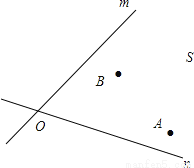
查看答案和解析>>
科目: 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
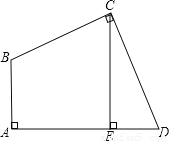
如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
查看答案和解析>>
科目: 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
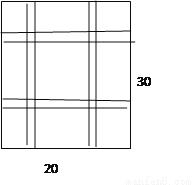
要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
查看答案和解析>>
科目: 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
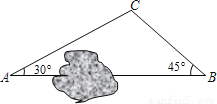
如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)
查看答案和解析>>
科目: 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量t(件),与每件的销售价x(元/件)可看成是一次函数关系:t=-3x+204.
(1)写出商场卖这种服装每天的销售利润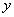 与每件的销售价
与每件的销售价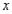 之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
当每件的销售价为55元时,可取得最大利润,每天最大销售利润为507元. 【解析】试题分析:(1)商场的利润是由每件商品的利润乘每天的销售的数量所决定.在这个问题中,每件服装的利润为(x-42),而销售的件数是(-3x+204),由销售利润y=(售价-成本)×销售量,那么就能得到一个y与x之间的函数关系,这个函数是二次函数. (2)要求销售的最大利润,就是要求这个二次函数的最大值. ...查看答案和解析>>
科目: 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2015年底拥有家庭轿车64辆,2017年底家庭轿车的拥有量达到100辆.
(1)若该小区2015年底到2018年底家庭轿车拥有量的年平均增长率都相同,求该小区到2018年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
方案一:建室内车位20个,露天车位50个;方案二:室内车位21个,露天车位45个. 【解析】试题分析:(1)设家庭轿车拥有量的年平均增长率为x,根据2015年底拥有家庭轿车64辆,2017年底家庭轿车的拥有量达到100辆列出方程,求出平均增长率,即可计算出2018年家庭轿车的数量; (2)设该小区可建室内车位a个,露天车位b个,根据总投资是15万元建立a、b的关系,然后用a去表示b,根...查看答案和解析>>
科目: 来源:山东省济南市2018届九年级1月月考数学试卷 题型:单选题
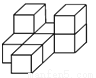
如图,由几个相同的小正方体搭成的一个几何体,它的左视图为( )
A. 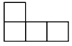 B.
B. 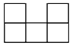 C.
C. 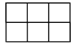 D.
D. 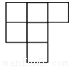
查看答案和解析>>
科目: 来源:山东省济南市2018届九年级1月月考数学试卷 题型:单选题
为估计池塘两岸A、B间的距离,晓明在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
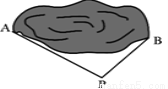
A. 5m B. 15m C. 20m D. 28m
D 【解析】【解析】 ∵PA、PB、AB能构成三角形,∴PA﹣PB<AB<PA+PB,即4m<AB<28m.故选D.查看答案和解析>>
科目: 来源:山东省济南市2018届九年级1月月考数学试卷 题型:单选题
如图,在△ABC中, 若DE∥BC , 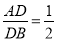 ,DE=4cm,则BC的长为 ( )
,DE=4cm,则BC的长为 ( )
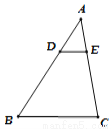
A. 8cm B. 12cm C. 11cm D. 10cm
B 【解析】试题分析:因为=,所以,又因为DE∥BC,所以, 因为DE=4cm,所以,所以BC=12cm,故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com