如图，用长为10米的篱笆，一面靠墙（墙的长度超过10米），围成一个矩形花圃，设矩形垂直于墙的一边长为x米，花圃面积为S平方米，则S关于x的函数解析式是 （不写定义域）．

【解析】矩形垂直于墙的一边长为x米，则另一边为（10?2 x）m， 所以花圃面积为S=x(10?2x)，即S=?2x2+10x； 故答案为：

如图，湖心岛上有一凉亭B，在凉亭B的正东湖边有一棵大树A，在湖边的C处测得B在北偏西45°方向上，测得A在北偏东30°方向上，又测得A、C之间的距离为100米，则A、B之间的距离是 米（结果保留根号形式）．

【解析】过点C⊥AB于点D, 在Rt△ACD中， ∵∠ACD=30°，AC=100m， ∴AD=100?sin∠ACD=100×=50(m)， CD=100?cos∠ACD=100×= (m) 在Rt△BCD中， ∵∠BCD=45°， ∴BD=CD=m， 则AB=AD+BD=50+ (m). 故答案为：50+

已知点（-1，m）、（2，n）在二次函数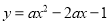的图像上，如果m>n，那么a 0（用“>”或“<”连接）．

>； 【解析】∵=a(x-1)2-a-1， ∴抛物线对称轴为：x=1， 由抛物线的对称性，点（-1，m）、（0，n）在二次函数的图像上， ∵-1<0，m>n， ∴当x<-1时，y随x的增大而减小，所以a>0. 故答案为：>

如图，已知在Rt△ABC中，∠ACB=90°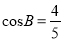，，BC=8，点D在边BC上，将△ABC沿着过点D的一条直线翻折，使点B落在AB边上的点E处，联结CE、DE，当∠BDE=∠AEC时，则BE的长是 .

【解析】如图作CH⊥AB于H. 在Rt△ABC中，∵BC=8， ， ∴AB=10，AC=8，CH=,BH=, 由题意EF=BF,设EF=BF=a,则BD=a, ∵∠BDE=∠AEC, ∴∠CED+∠ECB=∠ECB+∠B, ∴∠CED =∠B, ∵∠ECD=∠BCE, ∴△ECD∽△BCE, ∴EC2=CD·CB, ∴()2+(2a-)2...

将抛物线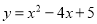向左平移4个单位，求平移后抛物线的表达式、顶点坐标

和对称轴．

，顶点坐标是（-2，1）；对称轴是直线． 【解析】试题分析：平移抛物线的依据是，当二次函数的二次项系数a的值相同时，二次函数图像的形状完全相同，即开口方向和开口大小完全相同，仅仅位置不同，所以他们之间可以进行平移. 试题解析：∵=， ∴平移后的函数解析式是． 顶点坐标是（-2，1）． 对称轴是直线．

如图，已知△ABC中，点D、E分别在边AB和AC上，DE∥BC，且DE经过△ABC的重心，设．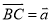

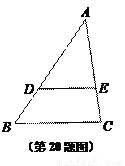
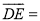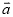（1） （用向量表示）；

（2）设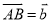，在图中求作．

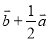（不要求写作法，但要指出所作图中表示结论的向量．）

（1）；（2）详见解析. 【解析】试题分析：（1）由DE∥BC，DE经过△ABC的重心，可得AD：AB=DE：BC=2：3，即可求得； （2）取点BC的中点M，连接AM，则即为所求. 试题解析：(1)∵DE∥BC，DE经过△ABC的重心， ∴AD：AB=DE：BC=2：3，， ∵， ∴ ； （2）如图,取点AB的中点M，连接AM，则即为所求.

如图，已知G、H分别是□ABCD对边AD、BC上的点，直线GH分别交BA和DC的延长线于点E、F．

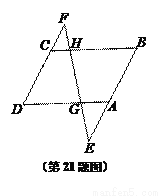
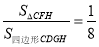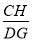（1）当时，求 的值；

（2）联结BD交EF于点M，求证：MG·ME=MF·MH.

（1）；（2）详见解析. 【解析】试题分析：（1）由，得.由于△CFH∽△DFG，由相似三角形面积的比等于相似比的平方，即可求得结果； （2）根据平行四边形的性质得出AB∥CD，AD//BC，由平行线分线段成比例得出比例式，即可得出答案. 试题解析：（1）∵， ∴． ∵ □ABCD中，AD//BC, ∴ △CFH∽△DFG ， ∴ ()2, ∴=． ...

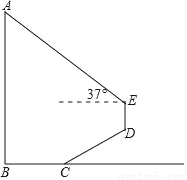
如图，为测量学校旗杆AB的高度，小明从旗杆正前方3米处的点C出发，沿坡度为i=1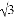：的斜坡CD前进2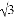米到达点D，在点D处放置测角仪，测得旗杆顶部A的仰角为37°，量得测角仪DE的高为1.5米．A、B、C、D、E在同一平面内，且旗杆和测角仪都与地面垂直．

（1）求点D的铅垂高度（结果保留根号）；

（2）求旗杆AB的高度（精确到0.1）．

（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75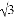，≈1.73．）

（1）点D的铅垂高度是米（2）旗杆AB的高度约为7.7米 【解析】试题分析：（1）延长ED交射线BC于点H，根据坡度为1：，可得∠DCH =30°，由直角三角形中30°角所对的边等于斜边的一半，得DH=； （2）求出EF和FB的值，在Rt△AEF中，由正切求得AF的值，即可求得AB的值． 试题解析：（1）延长ED交射线BC于点H.由题意得DH⊥BC. 在Rt△CDH中，∠D...

如图，已知，在锐角△ABC中，CE⊥AB于点E，点D在边AC上，联结BD交CE于点F，且EF·FC=FB·DF.

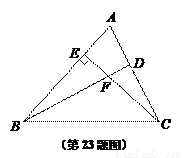
（1）求证：BD⊥AC；

（2）联结AF，求证：AF·BE=BC·EF.

（1）详见解析；（2）详见解析. 【解析】试题分析：（1）由两边成比例且夹角相等的两个三角形相似，可得△EFB∽△DFC，再由相似三角形对应角相等得∠FEB=∠FDC = 90°，即可得证； （2）由△EFB∽△DFC得∠ABD =∠ACE，进而△AEC∽△FEB，由相似三角形对应边成比例得，由此△AEF∽△CEB，可得. 试题解析：（1）∵AF·BE=BC·EF ， ∴，...

已知抛物线y＝ax2＋bx＋5与x轴交于点A(1，0)和点B(5，0)，顶点为M．点C在x轴的负半轴上，且AC＝AB，点D的坐标为(0，3)，直线l经过点C、D．

（1）求抛物线的表达式；

（2）点P是直线l在第三象限上的点，联结AP，且线段CP是线段CA、CB的比例中项，

求tan∠CPA的值；

（3）在（2）的条件下，联结AM、BM，在直线PM上是否存在点E，使得∠AEM=∠AMB.若存在，求出点E的坐标；若不存在，请说明理由．

（1）；（2） ；（3）E的坐标为（-2，-4）或（4，-4）. 【解析】试题分析：（1）把A、B两点带入抛物线解析式，求得a、b的值，即可得到抛物线解析式； （2）由AC=AB且点C在点A的左侧，及线段CP是线段CA、CB的比例中项，可得CP=， 由两边对应成比例且夹角相等的三角形相似，可得△CPA∽△CBP，由此∠CPA= ∠CBP. 过P作PH⊥x轴于H，易得PH=4...