
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:填空题
把二次函数y=x2-4x+5化成y=a(x-h)2+k的形式为__________________.
y=(x-2)2+1 【解析】∵, ∴二次函数化为顶点式为. 故答案为: .查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:填空题
数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°. 室外测量组测得BF的长度为5米.则旗杆AB=______米.
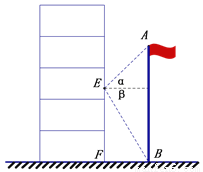
查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:填空题
在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为______________米2.
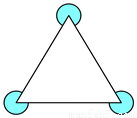
查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:填空题
阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.
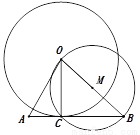
请回答:这样做的依据是__________________________________________________.
圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线. 【解析】∵要作出线段OB的中点M, ∴需作线段OB的垂直平分线,交OB于点M, ∴OM=MB(线段垂直平分线上的点到线段两端的距离相等); ∵以M为圆心,MO为半径作⊙M(圆的定义), ∴OB是⊙M的直径(直径定义), ...查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
计算:4sin45°-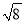 +(
+(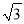 -1)0+|-2|.
-1)0+|-2|.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
如图,在△ABC中,D为AC边上一点,BC=4,AC=8,CD=2.求证:△BCD∽△ACB.

查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
如图,在△ABC中,tanA=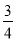 ,∠B=45°,AB=14. 求BC的长.
,∠B=45°,AB=14. 求BC的长.
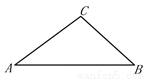
查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
在平面直角坐标系xOy中,直线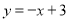 与双曲线
与双曲线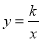 相交于点A(m,2).
相交于点A(m,2).
(1)求反比例函数的表达式;
(2)画出直线和双曲线的示意图;
(3)若P是坐标轴上一点,且满足PA=OA. 直接写出点P的坐标.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:

(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.

查看答案和解析>>
科目: 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.
(1)求证:AB=BN;
(2)若⊙O半径的长为3,cosB=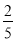 ,求MA的长.
,求MA的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com