
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:单选题
在Rt△ABC中, 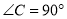 ,
, 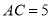 ,
, 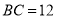 ,
, 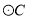 的半径为
的半径为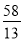 ,则
,则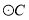 与
与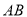 的位置关系是( )
的位置关系是( )
A. 相离 B. 相交 C. 相切 D. 无法确定
A 【解析】在Rt△ABC中, , , ,根据勾股定理求得AB=13,设斜边上的高为h,再根据直角三角形面积的两种表示法(即 )求得斜边上的高为,又因,即可得与相离,故选A.查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:单选题
动物学家通过大量调查估计:某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,活到30岁的概率为0.3,现年25岁的这种动物活到30岁的概率为( )
A. 0.3 B. 0.8 C. 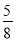 D.
D. 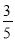
查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:单选题
已知抛物线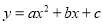 满足条件:(1)在
满足条件:(1)在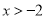 时,
时, 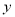 随
随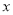 的增大而增大,在
的增大而增大,在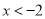 时,
时, 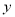 随
随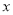 的增大而减小;(2)与
的增大而减小;(2)与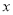 轴有两个交点,且两个交点间的距离小于
轴有两个交点,且两个交点间的距离小于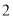 .以下四个结论:①
.以下四个结论:①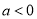 ;②
;②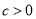 ;③
;③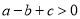 ;④
;④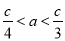 ,说法正确的个数有( )个
,说法正确的个数有( )个
A. 4 B. 3 C. 2 D. 1
B 【解析】由在时, 随的增大而增大,在时, 随的增大而减小,可得a>0,对称轴为x=-2;由与轴有两个交点,且两个交点间的距离小于,可得抛物线的图象与x轴的两个交点的横坐标位于-3与-1之间, 据条件得图象: , 观察图象可知,c>0, (当x=-1时,y=a-b+c>0);当x=-3时,y=9a-3b+c>0,由对称轴x=-2可得4a=b,所以9a-12a +c>0,即 ;又...查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:填空题
某抗菌素两年前每盒售价为20元,现在售价为12.8元,则该抗菌素的年平均下降率为___________.
20% 【解析】设每次降价的百分率为x,根据题意,可列方程20(1-x)2=12.8,解得x=0.2或x=1.8(舍去),即每次降价的百分率为20%.查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:填空题
已知⊙O半径为1,A、B在⊙O上,且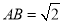 ,则AB所对的圆周角为___________.
,则AB所对的圆周角为___________.
查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:填空题
在平面直角坐标系中,将点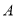 (2,-1)绕原点
(2,-1)绕原点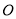 旋转
旋转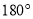 后,得到的对应点
后,得到的对应点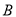 的坐标为___________.
的坐标为___________.
查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:填空题
如图,扇形纸扇完全打开后,外侧面两竹条AB、AC夹角为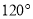 ,
, 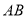 的长为
的长为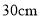 ,
, 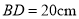 ,则扇面的面积为_____________cm2.
,则扇面的面积为_____________cm2.
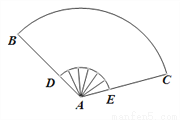
查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:填空题
已知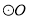 的内接正方形的面积为
的内接正方形的面积为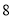 ,则
,则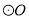 的内接正八边形的面积为__________.
的内接正八边形的面积为__________.
查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:填空题
已知直线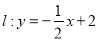 交
交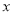 轴于
轴于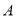 点,交
点,交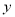 轴于
轴于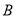 点,
点, 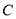 为
为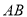 的中点,
的中点, 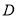 为射线
为射线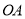 上一点,连
上一点,连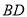 ,将
,将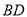 绕
绕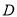 点顺时针旋转
点顺时针旋转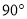 得线段
得线段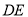 ,则
,则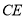 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
解方程: 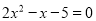
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com