
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
如果一幅地图的比例尺为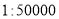 ,那么实际距离是
,那么实际距离是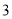 km的两地在地图上的图距是_________cm.
km的两地在地图上的图距是_________cm.
查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
如果抛物线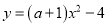 有最高点,那么a的取值范围是________.
有最高点,那么a的取值范围是________.
查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
抛物线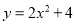 向左平移2个单位长度,得到新抛物线的表达式为_________.
向左平移2个单位长度,得到新抛物线的表达式为_________.
查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
已知点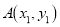 和
和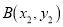 是抛物线
是抛物线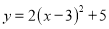 上的两点,如果
上的两点,如果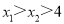 ,那么
,那么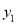 ______
______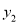 .(填“>”、“=”或“<”)
.(填“>”、“=”或“<”)
查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
在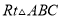 中,
中, 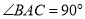 ,
, 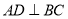 ,垂足为点D,如果
,垂足为点D,如果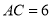 ,
, 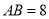 ,那么AD的长度为________.
,那么AD的长度为________.
查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
已知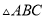 是等边三角形,边长为3,G是三角形的重心,那么GA的长度为___________.
是等边三角形,边长为3,G是三角形的重心,那么GA的长度为___________.
查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
正八边形的中心角的度数为__________度.
45 【解析】试题解析:正八边形的中心角等于360°÷8=45°; 故答案为:45°.查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
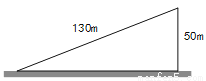
如图,一个斜坡长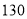 m,坡顶离水平地面的距离为
m,坡顶离水平地面的距离为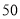 m,那么这个斜坡的坡度为_________.
m,那么这个斜坡的坡度为_________.
查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是_____________.

查看答案和解析>>
科目: 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
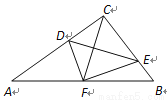
如图,在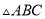 中,
中, 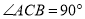 ,点D, E分别在
,点D, E分别在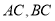 上,且
上,且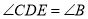 ,将
,将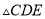 沿DE折叠,点C恰好落在AB边上的点F处,如果
沿DE折叠,点C恰好落在AB边上的点F处,如果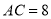 ,
, 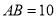 ,那么CD的长为__________.
,那么CD的长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com