
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
计算: 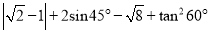 .
.
查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
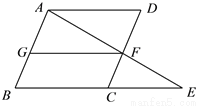
如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.
查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
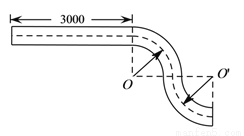
制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB的长为3 000mm,弯形管道部分BC,CD弧的半径都是1 000mm,∠O=∠O’=90°,计算图中中心虚线的长度.
查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
已知二次函数y=x2-4x+3.
(1)在网格中,画出该函数的图象.
(2)(1)中图象与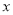 轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.

查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
已知:如图,在△ABC的中,AD是角平分线,E是AD上一点,且AB :AC = AE :AD.求证:BE=BD.
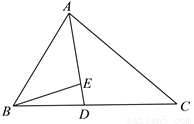
查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
如图所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米)
(参考数据:sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, 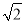 ≈1.41,
≈1.41, 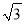 ≈1.73)
≈1.73)
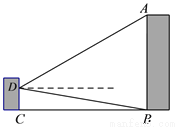
查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
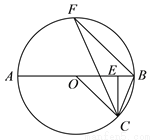
已知:如图, AB为⊙O的直径,CE⊥AB于E,BF∥OC,连接BC,CF.
求证:∠OCF=∠ECB.
查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
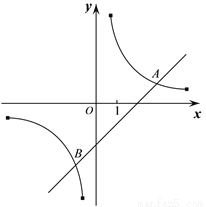
如图,在平面直角坐标系xOy中,直线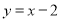 与双曲线
与双曲线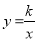 (k≠0)相交于A,B 两点,且点A的横坐标是3.
(k≠0)相交于A,B 两点,且点A的横坐标是3.
(1)求k的值;
(2)过点P(0,n)作直线,使直线与x轴平行,直线与直线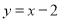 交于点M,与双曲线
交于点M,与双曲线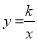 (k≠0)交于点N,若点M在N右边,求n的取值范围.
(k≠0)交于点N,若点M在N右边,求n的取值范围.
查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
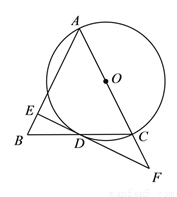
已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=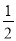 , CF=3,求DF的长.
, CF=3,求DF的长.
查看答案和解析>>
科目: 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.
(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB=__________;

(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;
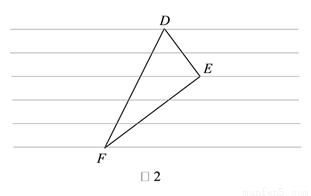
(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.
AB=; 【解析】试题分析:(1)如图,过点A、B分别作点C所在横线的垂线,垂足分别为D、E,然后证明△ADC≌△CEB,从而可得CE=AD=3,CD=BE=2,由勾股定理求得AC,BC的长,再由勾股定理即可求得AB的长; (2)如图所示,过点E作横线的垂线,然后证明△DME∽△ENF,再根据相似三角形的性质进行推导即可得; (3)连接DN与EG交于点P,根据相似三角形的性质即可...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com