
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
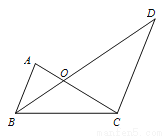
如图,BO是△ABC的角平分线,延长BO至D使得BC=CD.
(1)求证:△AOB∽△COD.
(2)若AB=2,BC=4,OA=1,求OC长.
查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
已知二次函数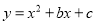 图象上部分点的横坐标
图象上部分点的横坐标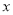 、纵坐标
、纵坐标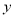 的对应值如下表:
的对应值如下表:

(1)求二次函数的表达式.
(2)画出二次函数的示意图,结合函数图象,直接写出y<0 时自变量x 的取值范围.
查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
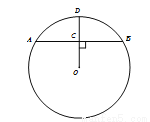
如图,AB是⊙O的弦,⊙O的半径OD⊥AB 垂足为C.若AB=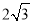 ,CD=1 ,求⊙O的半径长.
,CD=1 ,求⊙O的半径长.
查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
点P(1,4),Q(2, 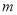 )是双曲线
)是双曲线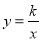 图象上一点.
图象上一点.
(1)求k值和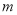 值.
值.
(2)O为坐标原点.过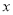 轴上的动点R作
轴上的动点R作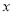 轴的垂线,交双曲线于点S,交直线OQ于点T,且点S在点T的上方.结合函数图象,直接写出R的横坐标
轴的垂线,交双曲线于点S,交直线OQ于点T,且点S在点T的上方.结合函数图象,直接写出R的横坐标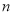 的取值范围.
的取值范围.
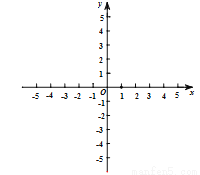
查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
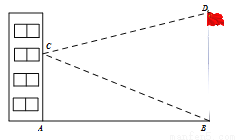
小明同学要测量学校的国旗杆BD的高度.如图,学校的国旗杆与教学楼之间的距AB=20m.小明在教学楼三层的窗口C测得国旗杆顶点D的仰角为14°,旗杆底部B的俯角为22°.
(1)求∠BCD的大小.
(2)求国旗杆BD的高度(结果精确到1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)
查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
如图,AB是⊙O的直径,C、D是⊙O上两点,弧AC=弧BC.过点B作⊙O的切线,连接AC并延长交于点E,连接AD并延长交于点F.
(1)求证:AC=CE;
(2)若AE=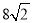 ,sin∠BAF=
,sin∠BAF=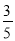 ,求DF长.
,求DF长.
查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
如图,Rt△ABC中, 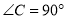 ,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为
,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为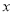 cm,BD长为
cm,BD长为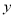 cm(当D与A重合时,
cm(当D与A重合时, 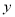 =4;当D与B重合时
=4;当D与B重合时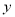 =0).
=0).
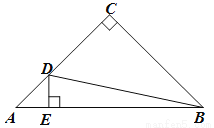
小云根据学习函数的经验,对函数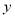 随自变量
随自变量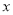 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小云的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了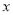 与
与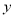 的几组值,如下表:
的几组值,如下表:
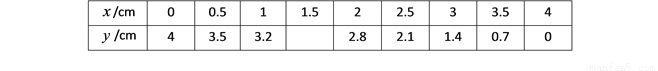
补全上面表格,要求结果保留一位小数.则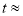 __________.
__________.
(2)在下面的网格中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当DB=AE时,AE的长度约为 cm.
(1)2.9;(2)答案见解析;(3)2.3. 【解析】试题分析:(1)通过取点、画图、测量,可得到结果; (2)通过描点,连线即可作出函数的图象; (3)根据题意可得当DB=AE时,AE的长度约为2.3cm. 试题解析:(1)2.9 (2)如图所示: (3)2.3查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
已知抛物线: 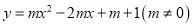 .
.
(1)求抛物线的顶点坐标.
(2)若直线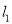 经过(2,0)点且与
经过(2,0)点且与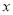 轴垂直,直线
轴垂直,直线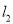 经过抛物线的顶点与坐标原点,且
经过抛物线的顶点与坐标原点,且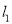 与
与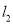 的交点P在抛物线上.求抛物线的表达式.
的交点P在抛物线上.求抛物线的表达式.
(3)已知点A(0,2),点A关于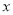 轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出
轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出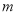 的取值范围.
的取值范围.
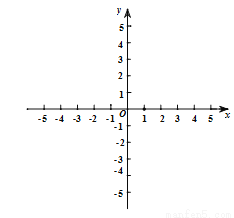
查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
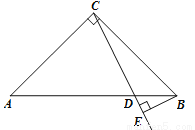
如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上的一点(不与A、B重合).过点B作BE⊥CD,垂足为E.将线段CE绕点C顺时针旋转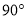 ,得到线段CF,连结EF.设∠BCE度数为
,得到线段CF,连结EF.设∠BCE度数为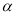 .
.
(1)①补全图形;
②试用含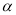 的代数式表示∠CDA.
的代数式表示∠CDA.
(2)若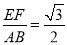 ,求
,求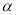 的大小.
的大小.
(3)直接写出线段AB、BE、CF之间的数量关系.
查看答案和解析>>
科目: 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
已知在平面直角坐标系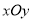 中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
(1)当⊙O的半径为1时:
①点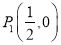 ,
,  ,
, 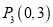 中,⊙O的关联点有_____________________.
中,⊙O的关联点有_____________________.
②直线经过(0,1)点,且与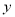 轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标
轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标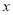 的取值范围.
的取值范围.
(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径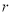 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com