
科目: 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:解答题
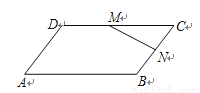
如图,已知平行四边形ABCD,点M、N分别是边DC、BC的中点,设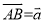 ,
, 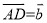 ,
,
求向量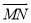 关于
关于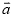 、
、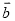 的分解式.
的分解式.
查看答案和解析>>
科目: 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:解答题
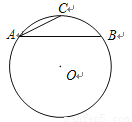
如图,已知AB是⊙O的弦,C是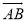 的中点,AB=8,AC=
的中点,AB=8,AC=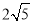 ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目: 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:解答题
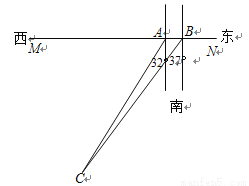
如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.
(参考数据:tan37°= cot53°≈0.755,cot37°= tan53°≈1.327,tan32°= cot58°≈0.625,cot32°= tan58°≈1.600.)
查看答案和解析>>
科目: 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:解答题
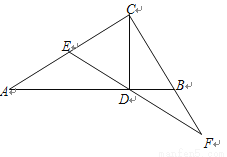
如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.
查看答案和解析>>
科目: 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:解答题
平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;
(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.
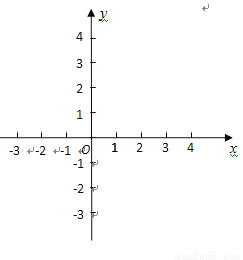
查看答案和解析>>
科目: 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:解答题
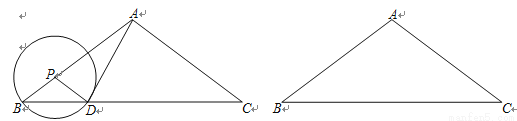
如图,已知在△ABC中,AB=AC=5,cosB=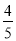 ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)求△ABC的面积;
(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△APD是直角三角形,求PB的长.
查看答案和解析>>
科目: 来源:北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型:单选题
在下面的四个有理数中,最小的是( )
A. ﹣1 B. 0 C. 1 D. ﹣2
D 【解析】∵-2<-1<0<1, ∴最小的数是-2, 故选D.查看答案和解析>>
科目: 来源:北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型:单选题
下列运算正确的是( )
A. 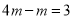 B.
B. 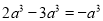 C.
C. 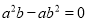 D.
D. 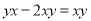
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com