
科目: 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图,已知直线AB和CD相交于点O,∠COE= 90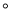 , OF平分∠AOE, ∠COF=28
, OF平分∠AOE, ∠COF=28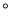 .求∠AOC的度数.
.求∠AOC的度数.
查看答案和解析>>
科目: 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,则应安排 ________名工人加工大齿轮,才能使每天加工的大小齿轮刚好配套.
25 【解析】【解析】 设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,由题意得: ,解得: .即安排25名工人加工大齿轮,才能使每天加工的大小齿轮刚好配套. 故答案为:25.查看答案和解析>>
科目: 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90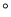 ).
).
(1)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由;
(2)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=60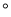 ,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目: 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
如图,已知菱形ABCD的周长为12,∠A=60°,则BD的长为( )
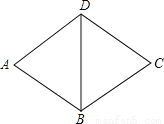
A. 3 B. 4 C. 6 D. 8
A 【解析】【解析】 ∵菱形ABCD的周长为12,∴菱形ABCD的边长=12÷4=3,∵∠A=60°,AD=AB,∴△ABD等边三角形,∴AB=BD,∴BD=3,故选A.查看答案和解析>>
科目: 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是( )
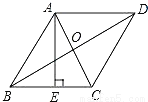
A. 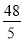 cm B.
cm B. 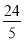 cm C.
cm C. 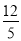 cm D.
cm D. 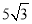 cm
cm
查看答案和解析>>
科目: 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
下列性质中,菱形对角线不具有的是( )
A. 对角线互相垂直 B. 对角线所在直线是对称轴
C. 对角线相等 D. 对角线互相平分
C 【解析】菱形的对角线互相垂直平分,菱形是轴对称图形,每一条对角线所在的直线就是菱形的一条对称轴, 故选C.查看答案和解析>>
科目: 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
菱形的两条对角线长分别为9cm与4cm,则此菱形的面积为( )cm2.
A. 12 B. 18 C. 20 D. 36
B 【解析】试题分析:根据对角线的长可以求得菱形的面积, 根据S=ab=×4cm×9cm=18cm2, 故选B.查看答案和解析>>
科目: 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
菱形ABCD的周长是20,对角线AC=8,则菱形ABCD的面积是( )
A. 12 B. 24 C. 40 D. 48
B 【解析】【解析】 ∵菱形ABCD的周长是20,∴AB=20÷4=5,AC⊥BD,OA=AC=4,∴OB= =3,∴BD=2OB=6,∴菱形ABCD的面积是: AC•BD=×8×6=24.故选B.查看答案和解析>>
科目: 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于( )
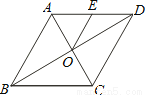
A. 4cm B. 5cm C. 6cm D. 8cm
C 【解析】试题分析:∵菱形ABCD的周长为48cm, ∴AD=12cm,AC⊥BD, ∵E是AD的中点, ∴OE=AD=6(cm). 故选:C.查看答案和解析>>
科目: 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:填空题
如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED= _____.
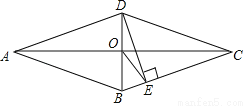
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com