
科目: 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
在宿州十一中校园文化艺术节中,九年级十班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
(1);(2) 【解析】试题分析:(1)直接根据概率公式求解; (2)画树状图展示所有12种等可能的结果数,再找出刚好是一男生一女生的结果数,然后根据概率公式求解. 试题解析:(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,刚好是男生的概率==; (2)画树状图为: 共有12种等可能的结果数,其中刚好是一男生一女生的结果数为6, 所以刚好是一男生一女生的...查看答案和解析>>
科目: 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(1)若 ,求CD的长;
,求CD的长;
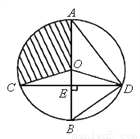
(2)若∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留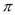 )。
)。
查看答案和解析>>
科目: 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
观察表格:根据表格解答下列问题:
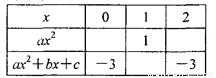
(l) a=______,b=_____,c=_____;
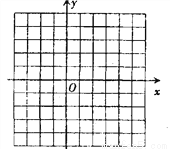
(2) 在右图的直角坐标系中画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c > -3成立;
(3)该图象与x轴两交点从左到右依次分别为A、B,与y轴交点为C,求过这三个点的外接圆的半径.
查看答案和解析>>
科目: 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价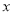 (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)
(2)当每盒售价定为多少元时,每天销售的利润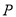 (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
查看答案和解析>>
科目: 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60cm,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿
CA方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与直线AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中:
(1)连接ME,当ME∥AC时,t=________s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
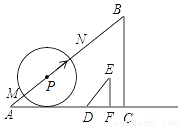
查看答案和解析>>
科目: 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).
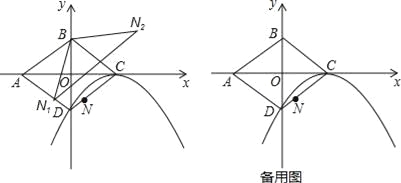
(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
(1)y=﹣(x﹣2)2(2)证明见解析(3)(4) 【解析】试题分析:(1)用待定系数法求,即可; (2)由对称的特点得出∠N1BN2=2∠DBC结合菱形的性质即可; (3)先判定出,当BN⊥CD时,BN最短,再利用△ABC∽△N1BN2得到比例式,求解,即可; (4)先建立PE=m2﹣m+2函数解析式,根据抛物线的特点确定出最小值. 试题解析:(1)由已知,设抛物...查看答案和解析>>
科目: 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:单选题
以下永洁环保、绿色食品、节能、绿色环保四个标志中,是轴对称图形是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:单选题
点P(2,﹣3)关于y轴的对称点的坐标是( )
A.(2,3) B.(﹣2,﹣3) C.(﹣2,3) D.(﹣3,2)
B 【解析】 试题分析:根据关于y轴对称的点,纵坐标相同,横坐标互为相反数解答. 【解析】 点P(2,﹣3)关于y轴的对称点的坐标是(﹣2,﹣3). 故选B.查看答案和解析>>
科目: 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:单选题
如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
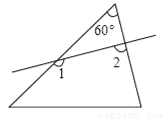
A. 120° B. 180° C. 240° D. 300°
C 【解析】根据三角形的内角和定理得: 四边形除去∠1,∠2后的两角的度数为180°﹣60°=120°, 则根据四边形的内角和定理得: ∠1+∠2=360°﹣120°=240°. 故选C.查看答案和解析>>
科目: 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:单选题
如图,在△ABC中,∠A=80°,∠B=40°,D,E分别是AB,AC上的点,且DE∥BC,则∠AED的度数为( )
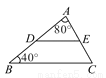
A. 40° B. 60° C. 80° D. 120°
B 【解析】试题分析:本题考查了三角形内角和定理、平行线的性质.解题时,要挖掘出隐含在题干中的已知条件:三角形的内角和是180°.根据两直线平行(DE∥BC),同位角相等(∠ADE=∠B)可以求得△ADE的内角∠ADE=40°;然后在△ADE中利用三角形内角和定理即可求得∠AED的度数.∵DE∥BC(已知),∠B=40°(已知),∴∠ADE=∠B=40°(两直线平行,同位角相等);又∵∠A=...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com