
科目: 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:填空题
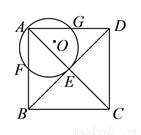
如图,在正方形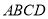 中,
中, 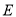 为对角线
为对角线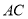 ,
, 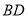 的交点,经过点
的交点,经过点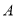 和点
和点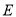 作⊙
作⊙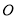 ,分别交
,分别交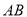 ,
, 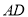 于点
于点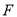 ,
, 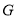 .已知正方形边长为
.已知正方形边长为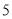 ,⊙
,⊙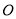 的半径为
的半径为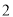 ,则
,则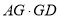 的值为__________.
的值为__________.
查看答案和解析>>
科目: 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
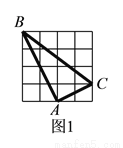
如图 ,在
,在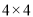 的正方形方格中,
的正方形方格中, 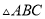 的顶点都在边长为
的顶点都在边长为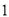 的小正方形的顶点.
的小正方形的顶点.
( )填空:
)填空: 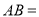 __________,
__________, 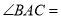 __________
__________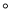 ;
;
(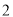 )请在图
)请在图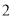 中的两个
中的两个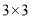 的正方形方格中各画一个和
的正方形方格中各画一个和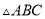 相似但不全等的格点三角形.
相似但不全等的格点三角形.

查看答案和解析>>
科目: 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
二次函数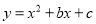 的图象经过点
的图象经过点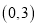 ,
, 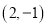 .
.
(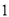 )求
)求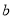 ,
, 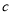 的值.
的值.
(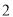 )求该二次函数图象的对称轴及与
)求该二次函数图象的对称轴及与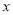 轴交点坐标.
轴交点坐标.
查看答案和解析>>
科目: 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
(本小题满分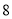 分)
分)
如图, 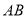 是⊙
是⊙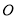 的直径,点
的直径,点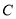 是⊙
是⊙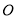 上一点,连接
上一点,连接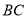 ,
, 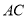 ,
, 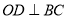 于
于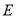 .
.
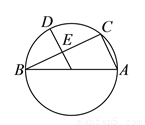
( )求证:
)求证: 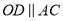 .
.
(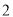 )若
)若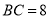 ,
, 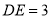 ,求⊙
,求⊙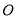 的直径.
的直径.
查看答案和解析>>
科目: 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
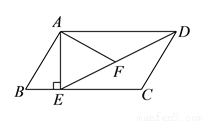
在平行四边形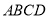 中,过点
中,过点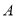 作
作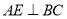 ,垂足为
,垂足为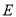 ,连接
,连接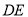 ,
, 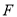 为线段
为线段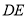 上一点,且
上一点,且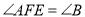 .
.
(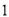 )求证:
)求证: 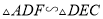 .
.
(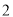 )若
)若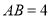 ,
, 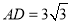 ,
, 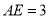 ,求
,求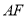 的长.
的长.
查看答案和解析>>
科目: 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: 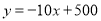 .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
(1)35;(2)30或40;(3)3600. 【解析】试题分析:(1)由题意得,每月销售量与销售单价之间的关系可近似看作一次函数,利润=(定价-进价)×销售量,从而列出关系式;(2)令w=2000,然后解一元二次方程,从而求出销售单价;根据抛物线的性质和图象,求出每月的成本. (1)由题意可得: w=(x-20)•y=(x-20)•(-10x+500)=-10x2+700x-1...查看答案和解析>>
科目: 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
如图所示, 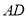 是
是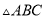 的角平分线,以点
的角平分线,以点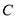 为圆心,
为圆心, 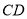 为半径作圆交
为半径作圆交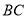 的延长线于点
的延长线于点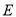 ,交
,交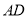 于点
于点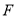 ,交
,交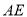 于点
于点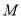 ,且
,且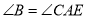 .
.
(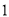 )求证:
)求证: 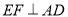 ;
;
(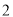 )求证:点
)求证:点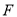 是
是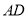 的中点;
的中点;
(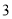 )如果
)如果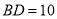 ,求半径
,求半径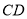 的长.
的长.

查看答案和解析>>
科目: 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
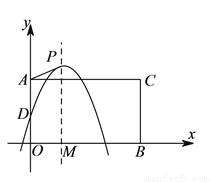
如图,在平面直角坐标系中,点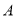 ,
, 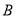 分别是
分别是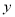 轴正半轴,
轴正半轴, 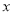 轴正半轴上两动点,
轴正半轴上两动点, 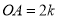 ,
, 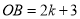 ,以
,以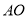 ,
, 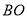 为邻边构造矩形
为邻边构造矩形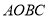 ,抛物线
,抛物线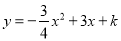 交
交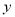 轴于点
轴于点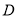 ,
, 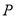 为顶点,
为顶点, 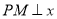 轴于点
轴于点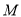 .
.
(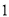 )求
)求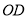 ,
, 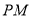 的长(结果均用含
的长(结果均用含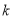 的代数式表示);
的代数式表示);
(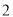 )当
)当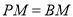 时,求该抛物线的表达式;
时,求该抛物线的表达式;
(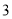 )在点
)在点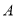 在整个运动过程中,若存在
在整个运动过程中,若存在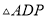 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的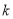 的值.
的值.
查看答案和解析>>
科目: 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列图形既是轴对称图形又是中心对称图形的是( )

A. A B. B C. C D. D
A 【解析】A选项中的图形既是轴对称图形,又是中心对称图形,所以可以选A; B选项中的图形既不是轴对称图形,又不是中心对称图形,所以不能选B; C选项中的图形既不是轴对称图形,又不是中心对称图形,所以不能选C; D选项中的图形是轴对称图形,但不是中心对称图形,所以不能选D; 故选A.查看答案和解析>>
科目: 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
用四舍五入法按要求对0.05049分别取近似值,其中错误的是( )
A. 0.1(精确到0.1) B. 0.05(精确到千分位)
C. 0.05(精确到百分位) D. 0.050(精确到0.00 1)
B 【解析】A选项,因为0.05049精确到0.1的结果是0.1,所以A中结果正确; B选项,因为0.05049精确到千分位的结果是0.050,所以B中结果错误; C选项,因为0.05049精确到百分位的结果是0.05,所以C中结果正确; D选项,因为0.05049精确到0.001的结果是0.050,所以D中结果正确; 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com