
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:填空题
如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于 .
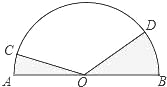
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:填空题
如图,在半径为3的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心运动路径的长度等于_____.
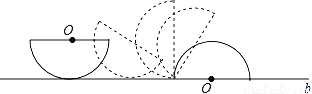
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:填空题
如图,已知一次函数y=﹣x+3的图象与坐标轴分别交于点A,B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PQ,切点为Q,则PQ的最小值为_____.
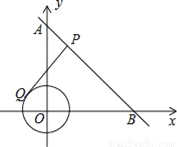
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
解下列方程:
(1)4x2=9;
(2)3y2﹣4y+1=0;
(3)(x+3)2=5(x+3);
(4)x2+3x﹣4=0 (配方法).
(1)x=±(2)y=1或y=(3)x=﹣3或x=2(4)x=1或x=﹣4 【解析】试题分析:(1)直接开平方法求解可得;(2)因式分解法求解可得;(3)因式分解法求解可得;(4)配方法求解可得. 解:(1)∵x2=, ∴x=±; (2)∵(y﹣1)(3y﹣1)=0, ∴y﹣1=0或3y﹣1=0, 解得:y=1或y=; (3)∵(x+3)2﹣5(x+3)=...查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数.
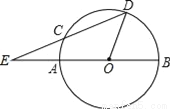
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
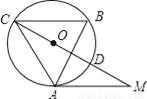
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
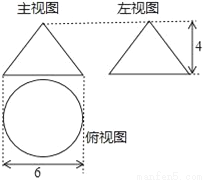
已知一个几何体的三视图如图,根据图示的数据计算该几何体的全面积及侧面展开图的圆心角(结果保留π).
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
用一根长22cm的铁丝:
(1)能否围成面积是30cm2的扇形?若能,求出扇形半径;若不能,请说明理由.
(2)能否围成面积是32cm2的扇形?并说明理由.
(1) cm;(2)cm. 【解析】试题分析:(1)可设扇形半径为xcm,根据等量关系:扇形的面积是30cm2列出方程求解即可; (2)可设扇形半径为ycm,根据等量关系:扇形的面积是32cm2列出方程求解即可. 解:(1)设扇形半径为xcm,依题意有 x(22﹣2x)=30, x2﹣11y+15=0, 解得x1=,x2=(舍去). 故扇形半径为cm; ...查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
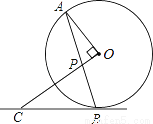
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为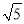 ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
如图,在平行四边形ABCD中,以A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若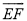 的长为
的长为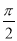 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
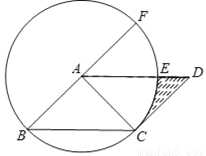
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com