
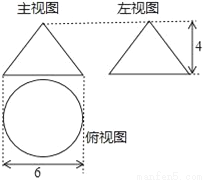
��֪һ�������������ͼ��ͼ������ͼʾ�����ݼ���ü������ȫ���������չ��ͼ��Բ�Ľǣ���������У���

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
���㣺 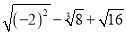 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�������³�������·���ʵ�������������ѧ�Ծ� ���ͣ���ѡ��
��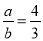 ����
����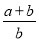 ��ֵ���ڣ� ����
��ֵ���ڣ� ����
A. 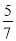 B.
B. 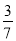 C.
C. 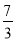 D.
D. 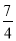
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�������ຼ��Ӣ�������ѧУ2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ���ѡ��
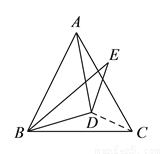
��ͼ�� 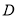 Ϊ�ȱ�
Ϊ�ȱ�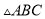 ���ڲ�һ�㣬
���ڲ�һ�㣬 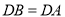 ��
�� 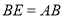 ��
�� 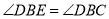 ����
����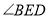 ���ڣ� ��
���ڣ� ��
A. 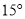 B.
B. 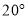 C.
C. 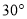 D.
D. 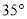
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����˽����֪˫��ѧУ2018����꼶���ϣ�������ѧģ���Ծ� ���ͣ������
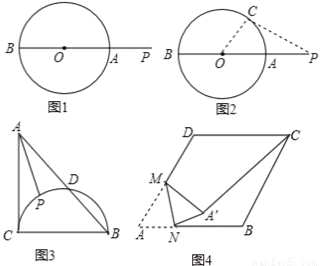
�Ķ����ϣ���ͼ1������P�ǡ�O���һ�㣬�߶�PO����O�ڵ�A����PA���ǵ�P���O�ϸ���֮�����̾��룮
֤�����ӳ�PO����O�ڵ�B����ȻPB��PA��
��ͼ2���ڡ�O����ȡһ��C�����A��B���غϣ�������PC��OC��
��PO��PC+OC��
��PO=PA+OA��OA=OC��
��PA��PC
��PA ���ǵ�P���O�ϸ���֮�����̾��룮
�ɴ˿��Եõ������⣺Բ��һ����Բ�ϸ���֮�����̾�������㵽Բ�ĵľ�����뾶�IJ�����������������������⣮
��1����ͼ3����Rt��ABC�У���ACB=90�㣬AC=BC=2����BCΪֱ���İ�Բ��AB��D��P��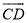 �ϵ�һ�����㣬����AP����AP������Сֵ���� ����
�ϵ�һ�����㣬����AP����AP������Сֵ���� ����
��2����ͼ4���ڱ߳�Ϊ2������ABCD�У���A=60�㣬M��AD�ߵ��е㣬��N��AB����һ���㣬����AMN��MN���ڵ�ֱ�߷��۵õ���A��MN������A��C�������߶�A��M�ij��ȣ� �����߶�A��C������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����˽����֪˫��ѧУ2018����꼶���ϣ�������ѧģ���Ծ� ���ͣ������
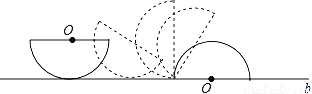
��ͼ���ڰ뾶Ϊ3�İ�Բ�ij�ʼ״̬��ֱ��ƽ���������ϵ�ֱ��b��Ȼ��Ѱ�Բ��ֱ��b��������������ʹ��Բ��ֱ����ֱ��b�غ�Ϊֹ����Բ���˶�·���ij��ȵ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����˽����֪˫��ѧУ2018����꼶���ϣ�������ѧģ���Ծ� ���ͣ���ѡ��
��ͼ��������ͼ�����μ����Ŀ飬ǡ��ƴ����ͼ�ľ��Σ���a=1����b=��������
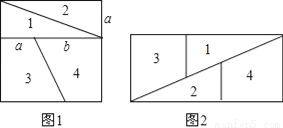
A. 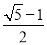 B.
B. 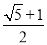 C.
C. 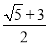 D.
D. 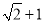
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�˲���2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
����ʽ�� �Ľ⼯��ʾ�������ϣ���ȷ���ǣ�������
�Ľ⼯��ʾ�������ϣ���ȷ���ǣ�������
A. 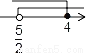 B.
B. 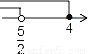 C.
C. 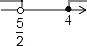 D.
D. 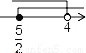
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��ͼ����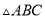 �У�
�� 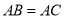 ����
����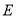 ��
��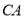 �ӳ����ϣ�
�ӳ����ϣ� 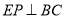 �ڵ�
�ڵ�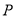 ����
����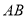 �ڵ�
�ڵ�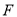 ��
��
��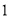 ����֤��
����֤�� 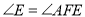 ��
��
��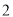 ����
����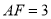 ��
�� 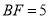 ����
����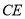 �ij���
�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com